【题目】如图,已知正方形ABCD,将一块等腰直角三角板的锐角顶点与A重合,并将三角板绕A点旋转,如图1,使它的斜边与BD交于点H,一条直角边与CD交于点G.
(1)请适当添加辅助线,通过三角形相似,求出![]() 的值;
的值;
(2)连接GH,判断GH与AF的位置关系,并证明;
(3)如图2,将三角板旋转至点F恰好在DC的延长线上时,若AD=![]() ,AF=
,AF=![]() .求DG的长.
.求DG的长.

参考答案:
【答案】(1)![]() ;(2)GH⊥AF,理由见解析;(3)
;(2)GH⊥AF,理由见解析;(3)![]()
【解析】试题分析:(1)连接AC,利用等量代换,求出∠BAH=∠GAC,再加上45的角,即可求出△BAH∽△CAG,进而得出结论;(2)先回答位置关系GH⊥AF,再证明,利用(1)问的结论,利用两边对应成比例且夹角相等得出△HAG∽△EAF,得出比例式即可;(3)判断出△AGD∽△FGE,得出![]() ,设出未知数,求出AG、EG的长度,利用相似即可求出DG的长度.
,设出未知数,求出AG、EG的长度,利用相似即可求出DG的长度.
试题解析:
(1)连接AC
∵四边形ABCD是正方形
∴∠BAC=∠ABH=∠ABH=45, ![]()
又∵△AEF是等腰直角三角形
∴∠EAH=45
∴∠BAH+∠EAC=∠FAC+∠EAC=45
∴∠BAH=∠GAC
∴△BAH∽△CAG.
∴![]()
(2)GH⊥AF,理由如下:
∵在Rt△AEF中, ![]()
∴![]()
又∵∠HAG=∠EAF
∴△HAG∽△EAF.
∴∠AHG=∠E=90
∴GH⊥AF..
(3)∵在Rt△AGH中, ![]()
∴AG=![]() GH
GH
又∵∠ADG=∠E=90,∠AGD=∠FGE
∴△AGD∽△FGE
∴![]() .
.
又∵在Rt△AEF中,AF=![]()
∴EF=5
∴![]()
∴![]()
∴![]()
∴可设GH为![]() ,则
,则![]()
∴AF=AH+FH=![]()
∴![]()
∴AG=![]() GH
GH![]()
∴![]()
又∵![]()
∴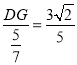
∴DG=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中,正确的是( )
A.两组对边分别平行的四边形是矩形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.一组邻边相等的矩形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】代数式2a+b表示的实际意义: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(k﹣3)x﹣k+2=0.
(1)若方程有一个根是0,求k的值.
(2)求证:无论k为何值,方程总有两个实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是随机事件的是( )
A.画一个三角形,使其内角和为181°B.明天太阳从西边升起
C.任取一个实数,与其相反数之和为0D.外观相同的10件产品中有两件不合格产品,现从中抽取一件恰为合格品.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2a2bm+1与﹣3anb2是同类项,则(﹣m)n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励居民节约用电,某省试行阶梯电价收费制,具体执行方案如下:
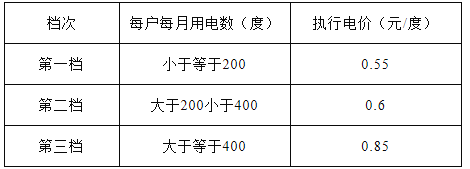
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).
某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
相关试题

