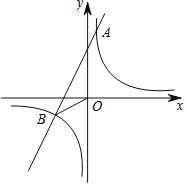
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A(1,8)、B(-4,m).
的图象交于点A(1,8)、B(-4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() 的解集;
的解集;
(4)若M(x1,y1)、N(x2,y2)是反比例函数![]() 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
参考答案:
【答案】(1)k1=8,k2=2,b=6;(2)15;(3)-4<x<0或x>1;(4)M(x1,y1)在第三象限,N(x2,y2)在第一象限.
【解析】试题分析:
(1)先把点A、B的坐标代入反比例函数的解析式求得k1和m的值,从而可得反比例函数的解析式和点B的纵坐标;再把点A、B的坐标代入![]() 列方程组可解得k2和b;
列方程组可解得k2和b;
(2)如图,连接OA,由(1)中所求一次函数的解析式求得直线AB与y轴的交点坐标C的坐标,由S△AOB=S△BOC+S△AOC即可求出所求面积;
(3)观察图象找到一次函数图象在反比例函数图象之上部分所对应的自变量的取值范围即可;
(4)因为在反比例函数中,k1=8>0,所以在每个象限内,反比例函数值y都随x的增大而减小,所以点M、N位于不同的分支上,结合x1<x2,y1<y2即可得到答案.
试题解析:
(1)∵反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m),
与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m),
∴k1=1×8=8,m=8÷(-4)=-2,
∴点B的坐标为(-4,-2).
将A(1,8)、B(-4,-2)代入y2=k2x+b中,
![]() ,解得:
,解得: ![]() .
.
∴k1=8,k2=2,b=6;
(2)如图,连接OA,设直线AB和y轴相交于点C,
∵当x=0时,y2=2x+6=6,
∴直线AB与y轴的交点C的坐标为(0,6).
∴S△AOB=S△BOC+S△AOC![]() ×6×4+
×6×4+![]() ×6×1=15;
×6×1=15;
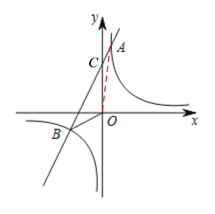
(3)观察函数图象可知:当-4<x<0或x>1时,一次函数的图象在反比例函数图象的上方,
∴不等式![]() <k2x+b的解为:-4<x<0或x>1;
<k2x+b的解为:-4<x<0或x>1;
(4)∵比例函数y=![]() 的图象位于第一、三象限,
的图象位于第一、三象限,
∴在每个象限内,y随x的增大而减小,
∵x1<x2,y1<y2,
∴M,N在不同的象限,
∴M(x1,y1)在第三象限,N(x2,y2)在第一象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
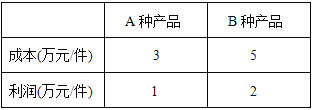
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知点A(0,a),B(0,b)在y轴上,点 C(m,b)是第四象限内一点,且满足
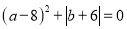 ,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.(1)求C点坐标;
(2)如图2,连接DE,若DE
 AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;
AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;(3)如图3,E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分 ∠AEC,且PM⊥EM于M点,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程中,
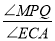 的大小是否发生变化,若不变,求出其值;若变化,请说明理由.
的大小是否发生变化,若不变,求出其值;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=
 ,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求
 的值;
的值;(2)当
 时,求
时,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=
 ,AE=3,求AF的长.
,AE=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=-x2+ax+b的图象与x轴交于A(-
 ,0),B(2,0)两点,且与y轴交于点C.
,0),B(2,0)两点,且与y轴交于点C.(1)求该抛物线的解析式,并判断△ABC的形状;
(2)设P是x轴上方的抛物线上的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、A 、M为顶点的三角形与ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )

①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
相关试题

