【题目】如图1,在平面直角坐标系中,已知点A(0,a),B(0,b)在y轴上,点 C(m,b)是第四象限内一点,且满足![]() ,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
(1)求C点坐标;
(2)如图2,连接DE,若DE![]() AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;
AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;
(3)如图3,E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分 ∠AEC,且PM⊥EM于M点,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程中,![]() 的大小是否发生变化,若不变,求出其值;若变化,请说明理由.
的大小是否发生变化,若不变,求出其值;若变化,请说明理由.

参考答案:
【答案】(1)a=8,b=-6, AB=14, BC=8, C(8,-6);(2)见解析;(3)![]()
【解析】
(1)根据非负数的性质求出a、b,得到点A、点B的坐标,根据△ABC的面积是56的面积公式求出CB,得到点C的坐标;(2)根据三角形内角和定理、“8字形”题、角平分线的定义计算即可;(2)因为EF为∠AED的平分线,∠DFE=90°,DE![]() AC,所以∠AEF=∠DEF=90°-∠FDE=∠ADF,又因为∠AEF=90°-∠OHE=90°-∠DHF=∠ODF
AC,所以∠AEF=∠DEF=90°-∠FDE=∠ADF,又因为∠AEF=90°-∠OHE=90°-∠DHF=∠ODF
所以∠ADF=∠ODF,可得FD平分∠ADO;(3)设∠AEM=∠CEM=![]() ,设∠APQ=∠NPQ=
,设∠APQ=∠NPQ=![]() ,因为PN∥AE ,由“M形”易得:(∠MPQ+∠NPQ)+∠AEM=∠M=90°, 即∠MPQ=90°-(
,因为PN∥AE ,由“M形”易得:(∠MPQ+∠NPQ)+∠AEM=∠M=90°, 即∠MPQ=90°-(![]() +
+![]() ),∠CPN+∠CEA=∠ECP=180-∠ECA , 即∠ECA=180-2(
),∠CPN+∠CEA=∠ECP=180-∠ECA , 即∠ECA=180-2(![]() +
+![]() )从而求解.
)从而求解.
解:(1)∵![]()
∴a-8=0,b+6=0,
解得a=8,b=-6,
∴A(3,0)、B(0,-4).
∴OA=8,OB=6,AB=14.
∵S△ABC=![]() ×BC×AB=
×BC×AB= ![]() ×BC×14=56,
×BC×14=56,
解得: BC=8,
∵C在第四象限,BC⊥y轴,
∴C(8,-6);
(2)∵EF为∠AED的平分线,∠DFE=90°,DE![]() AC
AC
∴∠AEF=∠DEF=90°-∠FDE=∠ADF
∠AEF=90°-∠OHE=90°-∠DHF=∠ODF
∴∠ADF=∠ODF,即FD平分∠ADO;
(3)设∠AEM=∠CEM=![]() ,设∠APQ=∠NPQ=
,设∠APQ=∠NPQ=![]() ,
,
∵PN∥AE 由“M形”易得:(∠MPQ+∠NPQ)+∠AEM=∠M=90°, 即∠MPQ=90°-(![]() +
+![]() ),∠CPN+∠CEA=∠ECP=180-∠ECA , 即∠ECA=180-2(
),∠CPN+∠CEA=∠ECP=180-∠ECA , 即∠ECA=180-2(![]() +
+![]() )
)
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=mx+n与
 ,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )
,其中m≠0,n≠0,那么它们在同一坐标系中的图象可能是( )A.
 B.
B. C.
C.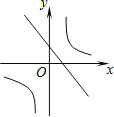 D.
D.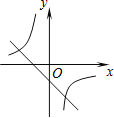
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
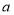 ∥
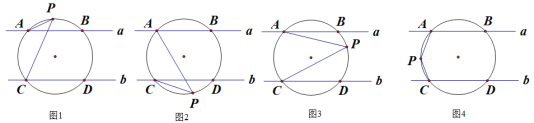
∥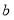 ,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.
,一圆交直线a,b分别于A、B、C、D四点,点P是圆上的一个动点,连接PA、PC.(1)如图1,直接写出∠PAB、∠PCD、∠P之间的数量关系为 ;
(2)如图2,直接写出∠PAB、∠PCD、∠P之间的数量关系为
(3)如图3,求证:∠P=∠PAB+∠PCD;
(4)如图4,直接写出∠PAB、∠PCD、∠P之间的数量关系为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
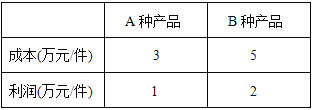
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=
 ,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求
 的值;
的值;(2)当
 时,求
时,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
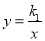 与一次函数
与一次函数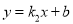 的图象交于点A(1,8)、B(-4,m).
的图象交于点A(1,8)、B(-4,m).(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)请直接写出不等式
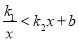 的解集;
的解集;(4)若M(x1,y1)、N(x2,y2)是反比例函数
 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.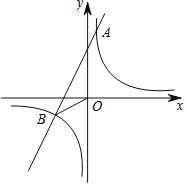
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=
 ,AE=3,求AF的长.
,AE=3,求AF的长.
相关试题

