【题目】阅读下列材料:
利用完全平方公式,可以将多项式![]() 变形为
变形为![]() 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式![]() 的配方法.
的配方法.
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:

![]()
![]()
根据以上材料,解答下列问题:
(1)用多项式的配方法将![]() 化成
化成![]() 的形式;
的形式;
(2)利用上面阅读材料的方法,把多项式![]() 进行因式分解;
进行因式分解;
(3)求证:![]() ,
,![]() 取任何实数时,多项式
取任何实数时,多项式![]() 的值总为正数.
的值总为正数.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据题意,利用配方法进行解答,即可得到答案;
(2)根据题意,根据材料的方法进行解答,即可得到答案;
(3)利用配方法把代数式进行化简,然后由完全平方的非负性,即可得到结论成立.
解:(1)![]()
=![]()
![]() ;
;
(2)![]()
![]()
![]()
![]()
![]() ;
;
(3)证明:![]()
![]()
![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() 的值总是正数.
的值总是正数.
即![]() 的值总是正数.
的值总是正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=
 ;④S△AEF=
;④S△AEF= .其中正确的有( )
.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.

A. 1 B. 2 C. 3 D.4
-
科目: 来源: 题型:
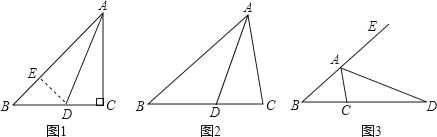
查看答案和解析>>【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
-
科目: 来源: 题型:
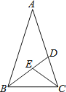
查看答案和解析>>【题目】如图,等腰
 中,腰
中,腰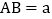 ,
,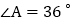 ,
,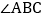 的平分线交
的平分线交 于
于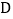 ,
,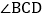 的平分线交
的平分线交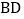 于
于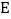 .设
.设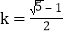 ,则
,则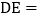 ( )
( )
A. k2a B. k3a C.
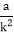 D.
D. 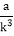
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊿
 中,
中, ,点
,点 分别在
分别在 边上,且
边上,且 ,
,  .
.⑴.求证:⊿
 是等腰三角形;
是等腰三角形;⑵.当
 时,求
时,求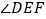 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解决下列两个问题:
(1)如图(1),在
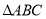 中,
中,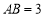 ,
,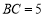 ,
,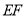 垂直平分
垂直平分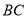 ,点
,点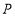 在直线
在直线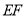 上,直接写出
上,直接写出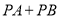 的最小值,并在图中标出当
的最小值,并在图中标出当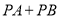 取最小值时点
取最小值时点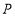 的位置;
的位置;(2)如图(2),点
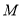 ,
,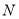 在
在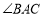 的内部,请在
的内部,请在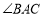 的内部求作一点
的内部求作一点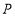 ,使得点
,使得点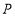 到
到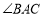 两边的距离相等,且使
两边的距离相等,且使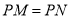 .(尺规作图,保留作图痕迹,无需证明).
.(尺规作图,保留作图痕迹,无需证明).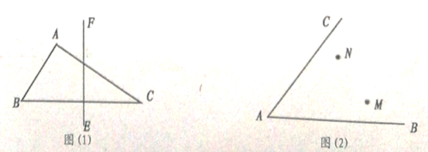
相关试题

