搜索
【题目】如图，在⊿
中，
,点
分别在
边上，且
, 
.
⑴.求证：⊿
是等腰三角形；
⑵.当
时，求
的度数.
参考答案：
【答案】（1）证明见解析；（2）70°
【解析】试题分析：（1）由AB=AC，∠ABC=∠ACB，BE=CF，BD=CE．利用边角边定理证明△DBE≌△CEF，然后即可求证△DEF是等腰三角形．
（2）根据∠A=40°可求出∠ABC=∠ACB=70°根据△DBE≌△CEF，利用三角形内角和定理即可求出∠DEF的度数．
试题解析：证明：∵AB=AC，∴∠ABC=∠ACB．在△DBE和△CEF中，∵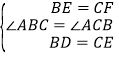
，∴△DBE≌△CEF，∴DE=EF，∴△DEF是等腰三角形；
（2）∵△DBE≌△CEF，∴∠1=∠3，∠2=∠4．∵∠A+∠B+∠C=180°，∴∠B=
（180°﹣40°）=70°，∴∠1+∠2=110°，∴∠3+∠2=110°，∴∠DEF=70°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
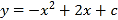与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是小明利用等腰直角三角板测量旗杆高度的示意图．等腰直角三角板的斜边BD与地面AF平行，当小明的视线恰好沿BC经过旗杆顶部点E时，测量出此时他所在的位置点A与旗杆底部点F的距离为10米．如果小明的眼睛距离地面1.7米，那么旗杆EF的高度为（ ）
A. 10米 B. 11.7米 C. 10
米 D. (5+1.7)米 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD为等边△ABC的高，E、F分别为线段AD、AC上的动点，且AE＝CF，当BF+CE取得最小值时，∠AFB＝（ ）
A. 112.5°B. 105°C. 90°D. 82.5°
-
科目： 来源： 题型：
查看答案和解析>>【题目】为适应新中考英语听说机考，九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩．甲、乙两位同学的练习成绩统计结果如图所示：
下列说法正确的是（ ）
A. 甲同学的练习成绩的中位数是38分
B. 乙同学的练习成绩的众数是15分
C. 甲同学的练习成绩比乙同学的练习成绩更稳定
D. 甲同学的练习总成绩比乙同学的练习总成绩低
-
科目： 来源： 题型：
查看答案和解析>>【题目】某移动通讯公司有两种移动电话计费方式，这两种计费方式中月使用费y（元）与主叫时间x（分）的对应关系如图所示：（主叫时间不到1分钟，按1分钟收费）下列三个判断中正确的是（ ）
①方式一每月主叫时间为300分钟时，月使用费为88元
②每月主叫时间为350分钟和600分钟时，两种方式收费相同
③每月主叫时间超过600分钟，选择方式一更省钱
A. ①② B. ①③ C. ②③ D. ①②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，一辆小汽车车门宽AO为1.2米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？______；(填“是”或“否”)请简述你的理由_______．(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84)
相关试题
