【题目】如图1,在平面直角坐标系中A(a,0),B(0,b),且a,b满足![]() .
.


(1) (2)
(1)A、B坐标分别为A( ) 、B( ).
(2)P为x轴上一点,C为AB中点,∠APC=∠PBO,求AP的长.
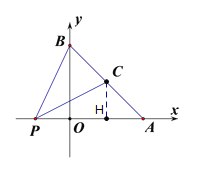
(3)如图2,点E为第一象限一点,AE=AB,以AE为斜边构造等腰直角△AFE,连BE,连接OF并延长交BE于点G,求证:BG=EG.
参考答案:
【答案】(1)A(4,0),B(0,4);(2)6;(3)见解析.
【解析】
(1)根据![]() 解出a,b的值,即可求出A,B的坐标;
解出a,b的值,即可求出A,B的坐标;
(2)作CH⊥AP于点H,由△AOB为等腰直角三角形,可证明∠PBC=∠PCB,从而证明△PBO≌△CPH,即可求出AP长;
(3)连接AG,根据题意证明△AOB≌△AFE,再根据角度转换得到∠BGO,∠AGO的度数,即可证明∠AGB=90°,即可证明BG=EG.
(1)由![]() 得:a=b=4,
得:a=b=4,
则点A坐标为(4,0),点B坐标为(0,4);
(2)作CH⊥AP于点H,
由(1)知△AOB为等腰直角三角形,
∴∠OBA=∠OAB=45°,
∵∠APC=∠PBO,
∴∠PCB=∠APC+∠CAP,∠PBC=∠PBO+∠OBA,
∴∠PBC=∠PCB,
∴PB=PC,
在△PBO和△CPH中
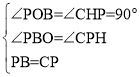
∴△PBO≌△CPH(AAS),
∵C为AB中点,
∴CH=2,
∴PO=CH=2,
∴AP=OA+OP=4+2=6;
(3)连接AG,
∵△AFE为等腰直角三角形,AE=AB,
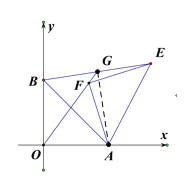
在△AOB和△AFE中
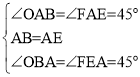
∴△AOB≌△AFE(ASA),
∴∠OAF=∠BAE,
∴∠FOA=∠EBA,
∴∠BGO=∠OAB=45°,
∴∠BOF=∠BAG,
∴∠AGO=∠OBA=45°,
∴∠BGA=90°,
∵△ABE为等腰三角形,
根据等腰三角形的三线合一知G为BE中点,
∴BG=EG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中
(1)求作:△ABC的内切圆⊙O(要求尺规作图,保留作图痕迹,不必写作法)
(2)综合应用:在你所作的圆中,若∠AOB=140°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是等边三角形,点E、F分别为射线AC、射线CB上两点,CE=BF,直线EB、AF交于点D.
(1)当E、F在边AC、BC上时如图,求证:△ABF≌△BCE.

(2)当E在AC延长线上时,如图,AC=10,S△ABC=25
 ,EG⊥BC于G,EH⊥AB于H,HE=8
,EG⊥BC于G,EH⊥AB于H,HE=8 ,EG= .
,EG= .
(3)E、F分别在AC、CB延长线上时,如图,BE上有一点P,CP=BD,∠CPB是锐角,求证:BP=AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果
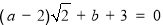 ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .(2)如果
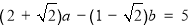 ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB延AE折叠刀AF,延长EF交DC于G,连接AG,现在有如下结论:①∠EAG=45°;②GC=CF;③FC∥AG;④S△GFC=14.4;其中结论正确的个数是( )

A.1B.2C.3D.4
-
科目: 来源: 题型:
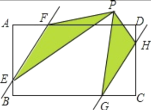
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=6,AB=5,点E、F、G、H分别在AD、AB、BC、CD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于______.
相关试题

