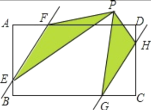
【题目】如图,在矩形ABCD中,AD=6,AB=5,点E、F、G、H分别在AD、AB、BC、CD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于______.
参考答案:
【答案】![]()
【解析】
连接EG,FH,可以证明△AEF≌△CGH,得EF=GH;同理可得EG=FH,进而得到四边形EGHF是平行四边形,所以△PEF和△PGH的面积和等于平行四边形EGHF的面积的一半,再利用平行四边形EGHF的面积等于矩形ABCD的面积减去四周四个小直角三角形的面积即可求解.
解:如图所示:
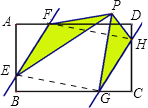
∵在矩形ABCD中,AD=6,AB=5,AF=CG=1,BE=DH=2,
∴AE=AB-BE=5-2=3,
CH=CD-DH=5-2=3,
∴AE=CH,
在△AEF与△CGH中,
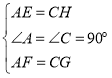 ,
,
∴△AEF≌△CGH(SAS),
∴EF=GH,
同理可得,△BGE≌△DFH,
∴EG=FH,
∴四边形EGHF是平行四边形,
∵△PEF和△PGH的高的和等于点H到直线EF的距离,
∴△PEF和△PGH的面积和=![]() 平行四边形EGHF的面积,
平行四边形EGHF的面积,
且平行四边形EGHF的面积=![]()
![]()
![]()
故△PEF和△PGH的面积和为:![]() .
.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中A(a,0),B(0,b),且a,b满足
 .
.

(1) (2)
(1)A、B坐标分别为A( ) 、B( ).
(2)P为x轴上一点,C为AB中点,∠APC=∠PBO,求AP的长.
(3)如图2,点E为第一象限一点,AE=AB,以AE为斜边构造等腰直角△AFE,连BE,连接OF并延长交BE于点G,求证:BG=EG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果
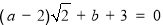 ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .(2)如果
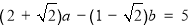 ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB延AE折叠刀AF,延长EF交DC于G,连接AG,现在有如下结论:①∠EAG=45°;②GC=CF;③FC∥AG;④S△GFC=14.4;其中结论正确的个数是( )

A.1B.2C.3D.4
-
科目: 来源: 题型:
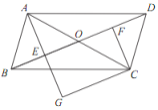
查看答案和解析>>【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择,其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调查,购买3台甲型机器和2台乙机器共需31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么该工厂有几种购买方案?
(3)在(2)的条件下,如果该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金,应选择那种方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线PA交⊙O于A、B两点,CD是⊙O的切线,切点且C,过点C作CD⊥PA于D,若AD:DC=1:3,AB=8,求⊙O的半径.

相关试题

