【题目】已知a是大于1的实数,且有a3+a-3=p,a3-a-3=q.
(1)若p+q=4,求p-q的值;
(2)当q2=22n+![]() -2(n≥1,且n是整数)时,比较p与a3+
-2(n≥1,且n是整数)时,比较p与a3+![]() 的大小.
的大小.
参考答案:
【答案】(1)p-q=1; (2)当n=1时,p>a3+![]() ;当n=2时,p=a3+
;当n=2时,p=a3+![]() ;当n≥3时,p<a3+
;当n≥3时,p<a3+![]() .
.
【解析】
(1)根据已知条件可得a=2,代入可求p-q的值;
(2)根据作差法得到p-(a+![]() )=
)=![]() ,分三种情况:当n=1时;当n=2时;当n≥3时进行讨论即可求解.
,分三种情况:当n=1时;当n=2时;当n≥3时进行讨论即可求解.
解:(1)∵a3+ a-3 =p①,a3-a-3=q②,
∴①+②得,2a3=p+q=4,∴a3=2,
①-②得,p-q=2a-3=1;
(2)∵q2=22n+2-2n-2(n≥1,且n是整数),
∴q2=(2n-2-n)2,∴q=2n-2-n.
又由(1)中①+②得2a3=p+q,a3=![]() (p+q),
(p+q),
①-②得,p-q=2a-3,a-3=![]() (p-q),
(p-q),
∴p2-q2=4,
p2=q2+4=(2n-2-n)2+4=(2n+2-n)2,
∴p=2n+2-n,
∴a3+a-3=2n+2-n,③
a3-a-3=2n-2-n,④
∴③+④得2a3=2×2n,
∴a3=2n,
∴p-(a3+![]() )=2n+2-n-2n-
)=2n+2-n-2n-![]() =2-n-
=2-n-![]() .
.
当n=1时,p>a3+![]() ;
;
当n=2时,p=a3+![]() ;
;
当n≥3时,p<a3+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
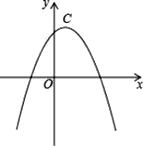
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )

A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,△BAC为等腰直角三角形,且∠BAC=90°.若点C恰好落在函数y=
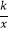 (x>0)在第一象限内的图象上,则k的值为( )
(x>0)在第一象限内的图象上,则k的值为( )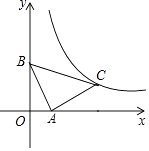
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为 .

相关试题

