【题目】如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.

参考答案:
【答案】FC2+BE2=EF2.
【解析】
BE2+CF2=EF2,可延长FD至P,使DP=DF,连接EP,连接BP,证明△CFD≌BPD,进而在Rt△PBE中,由勾股定理即可得出结论.
BE2+CF2=EF2.理由如下:
延长FD至P,使DP=DF,连接EP,BP.
∵D是BC的中点,∴BD=CD.
在△CDF和△BPD中,∵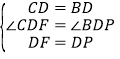 ,∴△CDF≌△BPD(SAS),∴CF=BP,∠C=∠PBD.
,∴△CDF≌△BPD(SAS),∴CF=BP,∠C=∠PBD.
∵∠A=90°,∴∠ABP=∠ABC+∠DBP=∠ABC+∠C=180°﹣90°=90°.
∵DE⊥DF,DF=DP,∴EF=FP(垂直平分线上的点到线段两端点距离相等).在Rt△BEP中,由勾股定理得:BE2+BP2=EP2=EF2,即:BE2+CF2=EF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程
(1)x2﹣4x+1=0 (2)(5x﹣3)2+2(3﹣5x)=0
(3)(2x+1)2=(x﹣1)2 (4)4x2+2=7x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=
 ,求⊙O的半径.
,求⊙O的半径.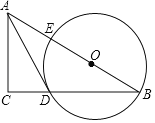
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
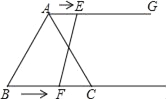
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,点F在线段CE上,且四边形BFED为菱形,则CF的为_____.
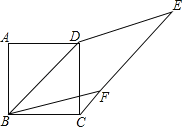
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
相关试题

