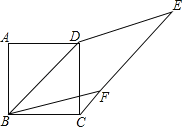
【题目】如图,正方形ABCD的边长为1,点F在线段CE上,且四边形BFED为菱形,则CF的为_____.
参考答案:
【答案】![]()
【解析】
过点F作FG⊥BC交BC延长线于G,根据正方形性质可得:BD=![]() ,∠CBD=45°,再由菱形性质可得:CE∥BD,BF=BD=
,∠CBD=45°,再由菱形性质可得:CE∥BD,BF=BD=![]() ,∠FCG=∠CBD=45°,因此△CFG是等腰直角三角形,设CG=FG=m,则CF=
,∠FCG=∠CBD=45°,因此△CFG是等腰直角三角形,设CG=FG=m,则CF=![]() m,由勾股定理可列方程求解.
m,由勾股定理可列方程求解.
解:如图,过点F作FG⊥BC交BC延长线于G,则∠CGF=90°
∵四边形ABCD是正方形
∴BC=CD=1,∠BCD=90°,∠CBD=45°,
∴BD=![]()
∵四边形BFED为菱形
∴CE∥BD,BF=BD=![]()
∴∠FCG=∠CBD=45°,
∴△CFG是等腰直角三角形,设CG=FG=m,则CF=![]() m
m
∴BG=1+m,
∵在Rt△BFG中,BG2+FG2=BF2
∴(1+m)2+m2=![]() ,解得:m1=
,解得:m1=![]() (舍去),m2=
(舍去),m2=![]() ,
,
∴CF=![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,点O在斜边AB上,以O为圆心,OB为半径作圆,分别与BC,AB相交于点D,E,连结AD.已知∠CAD=∠B.
(1)求证:AD是⊙O的切线.
(2)若BC=8,tanB=
 ,求⊙O的半径.
,求⊙O的半径.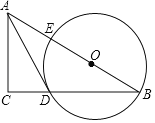
-
科目: 来源: 题型:
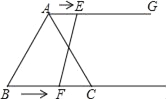
查看答案和解析>>【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率________.
②黑色方块所构拼图是中心对称图形的概率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在7×7网格中,每个小正方形的边长都为1.
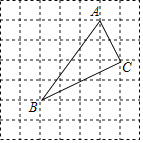
(1)建立适当的平面直角坐标系,使点A(3,4)、C(4,2),则点B的坐标为 ;
(2)求图中格点△ABC的面积;
(3)判断格点△ABC的形状,并说明理由.
(4)在x轴上有一点P,使得PA+PC最小,则PA+PC的最小值是 .
相关试题

