Question

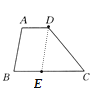
【题目】如图所示，AD∥BC，∠ABC＝80°，∠BCD＝50°，利用平移的知识讨论BC与AD+AB的数量关系．

Answer 1

【答案】BC＝AD+AB．

【解析】试题分析：把AB平移至DE的位置，由平移的性质可得：AB＝DE，AD＝BE，∠DEC＝∠ABC＝80°，在△DEC中利用三角形的内角和定理可得∠CDE＝∠BCD＝50°，再由等角对等边得出DE＝EC，等量代换即可得出结论．

试题解析：

解：由于AD∥BC，

所以可平移AB到DE的位置(即过D点作DE∥AB交BC于点E)，

则AB＝DE，AD＝BE，∠DEC＝∠ABC＝80°，

在△DEC中，由于∠BCD＝50 °，

所以∠CDE＝∠BCD＝50°，

因此DE＝EC，

所以BC＝BE＋EC＝AD＋DE＝AD＋AB．