搜索
【题目】如图，
与
是两个全等的等边三角形，
，下列结论不正确的是（ ）
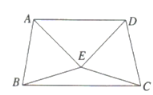
A.
B.直线
垂直平分
C.
D.四边形
是轴对称图形
参考答案：
【答案】A
【解析】
根据
与
是两个全等的等边三角形，可得到
，
，
，然后结合
，先计算出
的大小，便可计算出的大小，从而判定出AD与BC的位置关系及BE与DC的关系，同时也由于
与
是等腰三角形，也容易确定四边形ABCD的对称性．
（1）∵与是两个全等的等边三角形
∴，， 
∴
∵
∴
∴
，
∴
，所以选项A错误；
（2）由（1）得：
∴
∴
，所以选项C正确；
（3）延长BE交CD于点F，连接BD．
∵
，
∴
∴
∴
即
在
与
中
∴
∴
∴
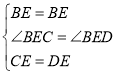
，综上，BE垂直平分CD,所以答案B正确；
（4）过E作
，由得
而
和
是等腰三角形，则MN垂直平分AD、BC，所以四边形ABCD是軕对称图形，所以选项Ｂ正确．
故选：Ａ
-
科目： 来源： 题型：
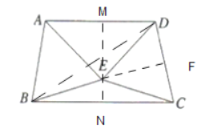
查看答案和解析>>【题目】在等腰直角三角形AOB中，已知AO⊥OB，点P、D分别在AB、OB上．
（1）∠A＝∠B＝ ；
（2）如图1中，若PO＝PD，∠OPD＝45°，证明△BOP是等腰三角形；
（3）如图2中，若AB＝10，点P在AB上移动，且满足PO＝PD，DE⊥AB于点E，试问：此时PE的长度是否变化？若变化，说明理由；若不变，求出PE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知抛物线y=x2+bx+c过A，B，C三点，点A的坐标是（3，0），点C的坐标是（0，-3），动点P在抛物线上．
（1）b =_________，c =_________，点B的坐标为_____________；（直接填写结果）
（2）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；
（3）过动点P作PE垂直y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】规定两数a，b之间的一种运算，记作（a，b）；如果ac＝b，那么（a，b）＝c，例如：因为23＝8，所以（2，8）＝3．
（1）根据上述规定，填空：（3，81）＝ ，（﹣
，﹣
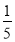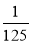）＝ ，（2，（2，256））＝ ；（2）若（3，4）+（3，6）＝（3，x），求x的值；
（3）证明：（2，3）+（2，5）＝（8，3375）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】ABCD为矩形的四个顶点，AB＝16 cm，AD＝6 cm，动点P、Q分别从点A、C同时出发，点P以3 cm/s的速度向点B移动，一直到达B为止，点Q以2 cm/s的速度向D移动，P、Q两点从出发开始到__________秒时，点P和点Q的距离是10 cm.
-
科目： 来源： 题型：
查看答案和解析>>【题目】讲授“轴对称”时，八年级教师设计了如下：四种教学方法：
① 教师讲，学生听
② 教师让学生自己做
③ 教师引导学生画图发现规律
④ 教师让学生对折纸，观察发现规律，然后画图
为调查教学效果，八年级教师将上述教学方法作为调研内容发到全年级8个班420名同学手中，要求每位同学选出自己最喜欢的一种．他随机抽取了60名学生的调查问卷，统计如图
(1) 请将条形统计图补充完整；
(2) 计算扇形统计图中方法③的圆心角的度数是 ；
(3) 八年级同学中最喜欢的教学方法是哪一种？选择这种教学方法的约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】现有A、B两种手机上网计费方式，收费标准如下表所示：
计费方式
月使用费/元
包月上网时间/分
超时费/(元/分)
A
30
120
0.20
B
60
320
0.25
设上网时间为x分钟，
(1)若按方式A和方式B的收费金额相等，求x的值；
(2)若上网时间x超过320分钟，选择哪一种方式更省钱？
相关试题
