【题目】在等腰直角三角形AOB中,已知AO⊥OB,点P、D分别在AB、OB上.
(1)∠A=∠B= ;
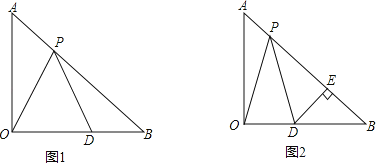
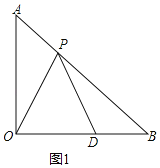
(2)如图1中,若PO=PD,∠OPD=45°,证明△BOP是等腰三角形;
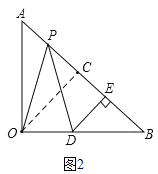
(3)如图2中,若AB=10,点P在AB上移动,且满足PO=PD,DE⊥AB于点E,试问:此时PE的长度是否变化?若变化,说明理由;若不变,求出PE的长.
参考答案:
【答案】(1)45°;(2)证明见解析;(3)PE的值不变,为5.
【解析】
(1)根据等腰直角三角形的定义可解答;
(2)由PO=PD,利用等边对等角和三角形内角和定理可求得∠POD=67.5°,∠OPB=67.5°,然后利用等角对等边可得出结论;
(3)过点O作OC⊥AB于C,首先利用等腰直角三角形的性质可以得到∠COB=∠B=45°,OC=5,然后证得∠POC=∠DPE,进而利用AAS证明△POC≌△DPE,再根据全等三角形的性质可得OC=PE.
(1)在等腰直角三角形AOB中,∠AOB=90°
∴∠A=∠B=45°
故答案为:45°;
(2)证明:∵PO=PD,∠OPD=45°,
∴∠POD=∠PDO=![]() =67.5°,
=67.5°,
由(1)知:∠B=45°,
∴∠OPB=180°﹣∠POB﹣∠B=67.5°,
∴∠POD=∠OPB,
∴BP=BO,即△BOP是等腰三角形;
(2)PE的值不变,证明如下:
如图2,过点O作OC⊥AB于C,
∵∠AOB=90°,AO=BO,
∴△BOC是等腰直角三角形,∠COB=∠B=45°,点C为AB的中点,
∴OC=![]() AB=5,
AB=5,
∵PO=PD,
∴∠POD=∠PDO,
又∵∠POD=∠COD+∠POC=45°+∠POC,∠PDO=∠B+∠DPE=45°+∠DPE,
∴∠POC=∠DPE,
在△POC和△DPE中,
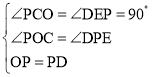 ,
,
∴△POC≌△DPE(AAS),
∴OC=PE=5,
∴PE的值不变,为5.
-
科目: 来源: 题型:
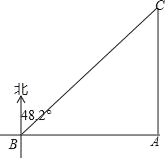
查看答案和解析>>【题目】如图,在一次海警演习中,A、B两地分别同时派出甲、乙两快艇营救一货轮C,已知B地位于A地正西方向相距84海里位置,货轮C位于A地正北方向,位于B地北偏东48.2°方向(所有数据精确到个位,sin48.2°≈0.7,cos48.2°≈0.6,tan48.2°≈1.05)
(1)求A、B两地分别与货轮C的距离;
(2)若乙快艇每小时比甲快艇多行驶20海里,且它们同时达到货轮C位置,求甲、乙快艇的速度.
-
科目: 来源: 题型:
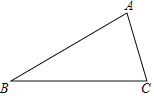
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=2∠B.
(1)作∠ACB的平分线交AB于D(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)若AB=10,AC=6,求△ACD的周长.
-
科目: 来源: 题型:
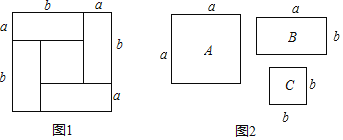
查看答案和解析>>【题目】利用图形面积可以解释代数恒等式的正确性,如图1可以验证一个代数恒等式(a+b)2=(a﹣b)2+4ab.
(1)如图2,用若干张A,B,C的卡片拼成一个长方形面积为(2a+b)(a+b),那么需要A,B,C卡片各多少张?
(2)如果用1张A,5张B,6张C拼成一个长方形,那么这个长方形的边长分别是 和 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】规定两数a,b之间的一种运算,记作(a,b);如果ac=b,那么(a,b)=c,例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(3,81)= ,(﹣
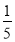 ,﹣
,﹣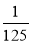 )= ,(2,(2,256))= ;
)= ,(2,(2,256))= ;(2)若(3,4)+(3,6)=(3,x),求x的值;
(3)证明:(2,3)+(2,5)=(8,3375).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
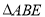 与
与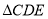 是两个全等的等边三角形,
是两个全等的等边三角形,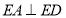 ,下列结论不正确的是( )
,下列结论不正确的是( )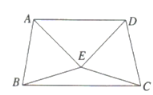
A.
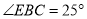 B.直线
B.直线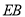 垂直平分
垂直平分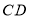
C.
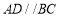 D.四边形
D.四边形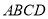 是轴对称图形
是轴对称图形
相关试题

