【题目】九年级(3)班数学兴趣小组经过市场调查整理发现某种商品的销售量P(件)与销售时间x天(1≤x≤90,且x为整数)成一次函数关系,具体数量关系如下表.已知商品的进价为30元/件,该商品的售价y(元/件)与销售时间x天的函数关系如图所示,每天的销售利润为w(元).

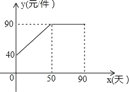
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
参考答案:
【答案】(1)w=![]() ;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)该商品在销售过程中,共有24天每天的销售利润不低于5600元.
;(2)销售第45天时,当天获得的销售利润最大,最大利润是6050元;(3)该商品在销售过程中,共有24天每天的销售利润不低于5600元.
【解析】分析:(1)当1≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b,由点的坐标利用待定系数法即可求出此时y关于x的函数关系式,根据图形可得出当50≤x≤90时,y=90.再结合给定表格,设每天的销售量p与时间x的函数关系式为p=mx+n,代入数据利用待定系数法即可求出p关于x的函数关系式,根据销售利润=单件利润×销售数量即可得出w关于x的函数关系式;
(2)根据w关于x的函数关系式,分段考虑其最值问题.当1≤x≤50时,结合二次函数的性质即可求出在此范围内w的最大值;当50≤x≤90时,根据一次函数的性质即可求出在此范围内w的最大值,两个最大值作比较即可得出结论;
(3)令w≥5600,可得出关于x的一元二次不等式和一元一次不等式,解不等式即可得出x的取值范围,由此即可得出结论.
详解:(1)当0≤x≤50时,设商品的售价y与时间x的函数关系式为y=kx+b.
∵y=kx+b经过点(0,40)、(50,90),∴![]() ,解得:
,解得:![]() ,∴售价y与时间x的函数关系式为y=x+40;
,∴售价y与时间x的函数关系式为y=x+40;
当50<x≤90时,y=90,∴售价y与时间x的函数关系式为y=![]() .
.
由每天的销售量p与时间x成一次函数关系,设每天的销售量p与时间x的函数关系式为p=mx+n.
∵p=mx+n过点(60,80)、(30,140),∴![]() ,解得:
,解得:![]() ,∴p=﹣2x+200(0≤x≤90,且x为整数),当0≤x≤50时,w=(y﹣30)p=(x+40﹣30)(﹣2x+200)=﹣2x2+180x+2000;
,∴p=﹣2x+200(0≤x≤90,且x为整数),当0≤x≤50时,w=(y﹣30)p=(x+40﹣30)(﹣2x+200)=﹣2x2+180x+2000;
当50<x≤90时,w=(90﹣30)(﹣2x+200)=﹣120x+12000.
综上所示,每天的销售利润w与时间x的函数关系式是
w=![]() .
.
(2)当0≤x≤50时,w=﹣2x2+180x+2000=﹣2(x﹣45)2+6050.
∵a=﹣2<0且0≤x≤50,∴当x=45时,w取最大值,最大值为6050元.
当50<x≤90时,
∵k=﹣120<0,w随x增大而减小,∴当x=50时,w取最大值,最大值为6000元.
∵6050>6000,∴当x=45时,w最大,最大值为6050元.
即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
(3)当1≤x≤50时,令w=﹣2x2+180x+2000≥5600,即﹣2x2+180x﹣3600≥0,解得:30≤x≤50,50﹣30+1=21(天);
当50≤x≤90时,令w=﹣120x+12000≥5600,即﹣120x+6400≥0,解得:50≤x≤53![]() .
.
∵x为整数,∴50≤x≤53,53﹣50+1=4(天).
综上可知:21+4﹣1=24(天),故该商品在销售过程中,共有24天每天的销售利润不低于5600元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点
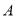 对应的数为
对应的数为  ,点
,点  对应的数为
对应的数为 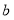 ,且多项式
,且多项式  的二次项系数为
的二次项系数为  ,常数项为
,常数项为 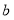 .
.(1)直接写出:
 ,
,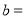 .
.(2)数轴上点
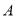 ,
, 之间有一动点
之间有一动点 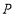 ,若点
,若点 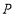 对应的数为
对应的数为 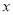 ,试化简
,试化简 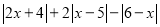 .
.(3)若点
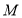 从点
从点 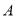 出发,以每秒
出发,以每秒  个单位长度的速度沿数轴向右移动;同时点
个单位长度的速度沿数轴向右移动;同时点 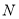 从点
从点  出发,沿数轴以每秒
出发,沿数轴以每秒 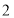 个单位长度的速度向左移动,到达
个单位长度的速度向左移动,到达 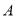 点后立即返回并向右继续移动,经过t秒后,
点后立即返回并向右继续移动,经过t秒后,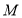 ,
, 两点相距
两点相距  个单位长度,求t的值.
个单位长度,求t的值. -
科目: 来源: 题型:
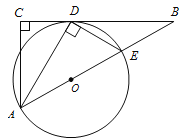
查看答案和解析>>【题目】已知:如图,在△ABC 中,∠C=90°,∠BAC 的平分线 AD 交 BC于点 D,过点 D 作 DE⊥AD 交 AB 于点 E,以 AE 为直径作⊙O.
(1)求证:BC 是⊙O 的切线;
(2)若 AC=3,BC=4,求 BE 的长.
(3)在(2)的条件中,求 cos∠EAD 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在数学活动课上,将边长为
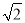 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
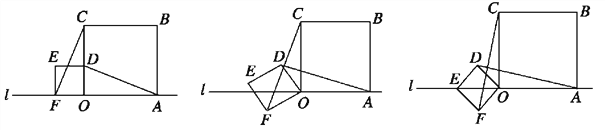
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
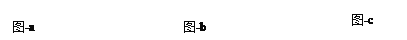
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,tanB=2。



(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF,求证:DF-EF=
 AF;
AF;(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论为____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
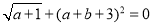 , ABCD的边AD与y轴交于点E,且E为AD中点,双曲线
, ABCD的边AD与y轴交于点E,且E为AD中点,双曲线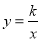 经过C、D两点.
经过C、D两点.(1)求k的值;
(2)点P在双曲线
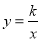 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;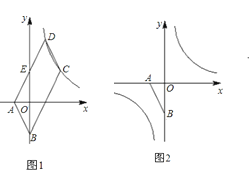
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班准备外出春游,有3名教师参加。有甲乙两家旅行社,其收费标准都一样,但都表示可以优惠师生.甲旅行社承诺:教师免费,学生按8折收费;乙旅行社承诺:师生一律按7折收费.
问:(1)如果由旅行社筹办春游活动,在什么条件下,两家旅行社所收费用相等.
(2)如果这个班有45名学生,选择哪家旅行社较恰当.请说明选择的理由.
相关试题

