【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。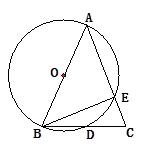
(1)求∠EBC的度数;
(2)求证:BD=CD。
参考答案:
【答案】
(1)解:∵AB为⊙O的直径,
∴∠AEB=∠CEB=90°,
又∵AB=AC,
∴∠ABC=∠ACB,
又∵∠BAC=45°,
∴∠ABC=∠ACB=67.5°,
∴∠EBC=90°-67.5°=22.5°,
(2)证明:连接AD,
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
即AD⊥BC,
又∵AB=AC,
∴BD=CD,
【解析】(1)由圆周角定理得出∠AEB=∠CEB=90°,又由等腰三角形的性质得出∠ABC=∠ACB,再根据三角形内角和得出∠ABC=∠ACB=67.5°,
∠EBC=22.5°.
(2)连接AD,由圆周角定理得出∠AEB=∠CEB=90°,即AD⊥BC;又由等腰三角形的性质得出BD=CD.
【考点精析】关于本题考查的三角形的内角和外角和等腰三角形的性质,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.
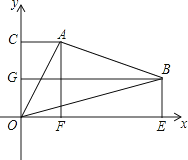
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程
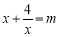 的两实根,且tan∠PCD=
的两实根,且tan∠PCD= ,求⊙O的半径.
,求⊙O的半径.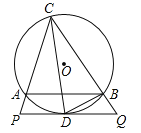
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )
A. ﹣5 B. ﹣3 C. 3 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=﹣2,则代数式a+1的值为( )
A.﹣3
B.﹣2
C.﹣1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠B与∠C的平分线交于点P.
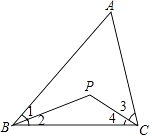
(1)当∠A=112°时,求∠BPC的度数;
(2)当∠A=α时,求∠BPC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形三个内角∠A、∠B、∠C,满足关系式∠B+∠C=2∠A,则此三角形( )
A. 一定有一个内角为45° B. 一定有一个内角为60°
C. 一定是直角三角形 D. 一定是钝角三角形
相关试题

