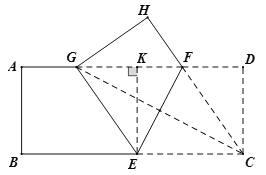
【题目】如图,将矩形纸片![]() (
(![]() )折叠,使点
)折叠,使点![]() 刚好落在线段
刚好落在线段![]() 上,且折痕分别与边
上,且折痕分别与边![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,设折叠后点
,设折叠后点![]() ,
,![]() 的对应点分别为点
的对应点分别为点![]() ,
,![]() .
.

(1)判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)若![]() ,且四边形
,且四边形![]() 的面积
的面积![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)四边形![]() 为菱形,理由见解析;(2)
为菱形,理由见解析;(2)![]()
【解析】
(1)根据折叠的性质可得EC=EG,GF=CF,![]() ,由GF∥EC,可得
,由GF∥EC,可得![]() ,进一步可得GE=GF,于是可得结论;
,进一步可得GE=GF,于是可得结论;
(2)根据题意可先求得CE的长,过点E作EK⊥GF于点K,在Rt△GEK中,根据勾股定理可求得GK的长,于是FK可求,在Rt△EFK中,再利用勾股定理即可求得结果.
(1)四边形![]() 为菱形,理由如下:
为菱形,理由如下:
证明:由折叠可得:![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形.
为菱形.
(2)如图,∵四边形![]() 为菱形,且其面积为
为菱形,且其面积为![]() ,∴
,∴![]() ,
,
∴![]() ,
,
过点E作EK⊥GF于点K,则EK=AB=4,
在Rt△GEK中,由勾股定理得:![]() ,
,
∴![]() ,
,
在Rt△EFK中,由勾股定理得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形 纸片的每个顶点与小正方形的顶点重合(如图①、图②、图③).


图②矩形(正方形)
 ,
,分别在图①、图②、图③中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把这两部分重新拼成符合下列要求的几何图形.
要求:
(1)在左边的平行四边形纸片中画一条裁剪线,然后在右边相对应的方格纸中,按实际大小画出所拼成的符合要求的几何图形.
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙.
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,以AO为直径作半圆M,C为OB的中点,D在半圆M上,且CD⊥MD,延长AD交半圆O于点E,且AB=4,则圆中阴影部分的面积为_____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲正在阅读《三国演义》,每天所读页数相同,当他读完第84页时,乙从头开始阅读同一本书籍,每天所读页数相同;下列表格记录了甲乙两人同读《三国演义》的进度.例如:第五天结束时,两人已读页数之和为424,此时甲比乙多读了24页;(注:已读页数中已计入了甲先读完的84页)
同读天数
1
2
3
4
5
已读页数之和
152
220
a
b
424
已读页数之差
72
60
48
36
24
(1)请直接写出表格中a、b的值;
(2)列方程求解:甲、乙两人每天各读书多少页?
(3)若这本书共有520页,从第6天起,甲每天比原来多读n页,乙每天所读页数不变,这样到第11天结束时,甲、乙两人已读页数相同,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错的题目进行整理、分析、改正” (选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为_______,
 ________ %,
________ %, ________%“很少”对应扇形的圆心角为_____________;
________%“很少”对应扇形的圆心角为_____________;(2)请补全条形统计图;
(3)若该校共有3500名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售单价分别为
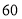 元/筒、
元/筒、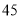 元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过
元/筒的甲、乙两种羽毛球.根据消费者需求,该网店决定用不超过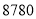 元购进甲、乙两种羽毛球共
元购进甲、乙两种羽毛球共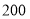 简.且甲种羽毛球的数量大于乙种羽毛球数量的
简.且甲种羽毛球的数量大于乙种羽毛球数量的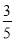 .已知甲、乙两种羽毛球的进价分别为
.已知甲、乙两种羽毛球的进价分别为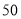 元/筒、
元/筒、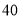 元/筒。若设购进甲种羽毛球
元/筒。若设购进甲种羽毛球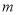 简.
简.(1)该网店共有几种进货方案?
(2)若所购进羽毛球均可全部售出,求该网店所获利润
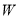 (元)与甲种羽毛球进货量
(元)与甲种羽毛球进货量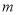 (简)之间的函数关系式,并求利润的最大值
(简)之间的函数关系式,并求利润的最大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】小莉的爸爸买了今年七月份去上海看世博会的一张门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,5的四张牌给小莉,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)请用数状图或列表的方法求小莉去上海看世博会的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
相关试题

