【题目】如图,AB为半圆O的直径,以AO为直径作半圆M,C为OB的中点,D在半圆M上,且CD⊥MD,延长AD交半圆O于点E,且AB=4,则圆中阴影部分的面积为_____________.

参考答案:
【答案】![]()
【解析】分析:
由CD为半圆M的切线,得到DC⊥MD,再由M为OA中点,C为OB中点,得到AM=MO=OC=BC=1,在Rt△DMC中,由DM=MO=OC=![]() MC可得∠DCM=30°,则∠DMC=60°结合AM=DM,可得∠MAD=∠OEA=30°,在Rt△AOD中,利用30度所对的直角边等于斜边的一半,求出OD的长,利用勾股定理求出AD的长,确定出AE的长,同理求出DF与AC的长,确定出∠EOB的度数,最后由S阴影=S△AOE+S扇形OEB-S△ACD,求出即可.
MC可得∠DCM=30°,则∠DMC=60°结合AM=DM,可得∠MAD=∠OEA=30°,在Rt△AOD中,利用30度所对的直角边等于斜边的一半,求出OD的长,利用勾股定理求出AD的长,确定出AE的长,同理求出DF与AC的长,确定出∠EOB的度数,最后由S阴影=S△AOE+S扇形OEB-S△ACD,求出即可.
详解:连接EO,DO,过点D作DF⊥AB于点F,
∵CD与半圆M相切,
∴CD⊥MD,
∵AB=4,O为AB的中点,M、C分别为AO、BO的中点,
∴AM=OM=OC=CB=1,
∵在Rt△MDC中,DM=MO=OC=![]() MC,
MC,
∴∠DCM=30°,
∴∠DMC=60°,
∵AM=DM,
∴∠MAD=∠MDA=30°,
∵OA=OE,
∴∠E=∠A=30°,
∴∠EOB=∠E+∠A=60°,OD=![]() OA=1,
OA=1,
∴AD=![]() ,
,
又∵OD⊥AE,
∴AE=2AD=![]() ,DF=
,DF=![]() AD=
AD=![]() ,
,
∴AF=![]() ,
,
∴AC=2AF=3,
∴S阴影=S△AOE+S扇形BOE-S△ACD
=![]() AE·OD+
AE·OD+![]() -
-![]() AC·DF
AC·DF
=![]() +
+![]() -
-![]()
=![]() .
.
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为
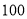 分.前
分.前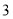 名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为
名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为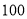 分),现得知
分),现得知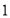 号选手的综合成绩为
号选手的综合成绩为 分.
分.序号
笔试成绩/分
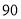
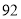
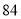
面试成绩/分

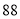
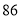
(1)求笔试成绩和面试成绩各占的百分比:
(2)求出其余两名选手的综合成绩,并以综合成绩排序确定这三名选手的名次。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形 纸片的每个顶点与小正方形的顶点重合(如图①、图②、图③).


图②矩形(正方形)
 ,
,分别在图①、图②、图③中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把这两部分重新拼成符合下列要求的几何图形.
要求:
(1)在左边的平行四边形纸片中画一条裁剪线,然后在右边相对应的方格纸中,按实际大小画出所拼成的符合要求的几何图形.
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙.
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲正在阅读《三国演义》,每天所读页数相同,当他读完第84页时,乙从头开始阅读同一本书籍,每天所读页数相同;下列表格记录了甲乙两人同读《三国演义》的进度.例如:第五天结束时,两人已读页数之和为424,此时甲比乙多读了24页;(注:已读页数中已计入了甲先读完的84页)
同读天数
1
2
3
4
5
已读页数之和
152
220
a
b
424
已读页数之差
72
60
48
36
24
(1)请直接写出表格中a、b的值;
(2)列方程求解:甲、乙两人每天各读书多少页?
(3)若这本书共有520页,从第6天起,甲每天比原来多读n页,乙每天所读页数不变,这样到第11天结束时,甲、乙两人已读页数相同,求n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片
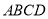 (
(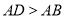 )折叠,使点
)折叠,使点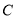 刚好落在线段
刚好落在线段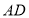 上,且折痕分别与边
上,且折痕分别与边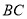 ,
,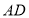 相交于点
相交于点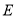 ,
,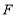 ,设折叠后点
,设折叠后点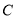 ,
,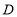 的对应点分别为点
的对应点分别为点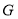 ,
,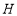 .
.
(1)判断四边形
 的形状,并证明你的结论;
的形状,并证明你的结论;(2)若
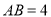 ,且四边形
,且四边形 的面积
的面积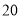 ,求线段
,求线段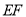 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错的题目进行整理、分析、改正” (选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为_______,
 ________ %,
________ %, ________%“很少”对应扇形的圆心角为_____________;
________%“很少”对应扇形的圆心角为_____________;(2)请补全条形统计图;
(3)若该校共有3500名学生,请你估计其中“总是”对错题进行整理、分析、改正的学生有多少名?
相关试题

