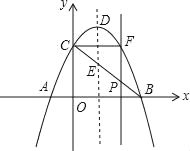
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D,连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点(P不与B,C两点重合),过点P作x轴的垂线交抛物线于点F,设点P的横坐标为m(0<m<3)
(1)当m为何值时,四边形PEDF为平行四边形;
(2)设△BCF的面积为S,求S的最大值.
参考答案:
【答案】(1)m=2(2)![]()
【解析】试题分析:(1)PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长. 根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
(2)可将△BCF分成两部分来求:一部分是△PFC,以PF为底边,以P的横坐标为高即可得出△PFC的面积. 一部分是△PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出△PFB的面积. 然后根据△BCF的面积=△PFC的面积+△PFB的面积,可求出关于S、m的函数关系式.
解:(1)对于抛物线y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点D(1,4)
令x=0,得到y=3;
令y=0,得到﹣x2+2x+3=0,即(x﹣3)(x+1)=0,
解得:x=﹣1或x=3,
则A(﹣1,0),B(3,0),C(0,3),抛物线对称轴为直线x=1;
设直线BC的函数解析式为y=kx+b,
把B(3,0),C(0,3)分别代入得:![]() ,
,
解得:k=﹣1,b=3,
∴直线BC的解析式为y=﹣x+3,
当x=1时,y=﹣1+3=2,
∴E(1,2),
∴DE=4﹣2=2,
∵PF⊥x轴,
∴P(m,﹣m+3),F(m,﹣m2+2m+3),
∴线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
连接DF,由PF∥DE,得到当PF=DE时,四边形PEDF为平行四边形,
由﹣m2+3m=2,得到m=2或m=1(不合题意,舍去),
当m=2时,四边形PEDF为平行四边形;
(2)∵B(3,0),
∴OB=3,
∴S=![]() PFOB=
PFOB=![]() ×3(﹣m2+3m)=﹣
×3(﹣m2+3m)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() (0<m<3),
(0<m<3),
则当m=![]() 时,S取得最大值为
时,S取得最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:﹣32÷(﹣3)2+3×(﹣2)+|﹣4|
(2)计算:
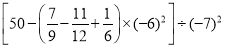
(3)化简:(5a2+2a﹣1)﹣4[3﹣2(4a+a2)]
(4)化简:3x2﹣[7x﹣(4x﹣3)﹣2x2]
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2
 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ;连接PQ,PQ与BC交于点E,QP延长线与AD(或AD延长线)交于点F,连接CQ.求证:
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ;连接PQ,PQ与BC交于点E,QP延长线与AD(或AD延长线)交于点F,连接CQ.求证:(1)CQ=AP;
(2)△APB∽△CEP.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师提出了一个问题:
如图1,A、B两点被池塘隔开,在AB外选一点,连接AC和BC,怎样测出A、B两点的距离?

【活动探究】学生以小组展开讨论,总结出以下方法:
(1)如图2,选取点C,使AC=BC=a,∠C=60°;
(2)如图3,选取点C,使AC=BC=b,∠C=90°;
(3)如图4,选取点C,连接AC,BC,然后取AC、BC的中点D、E,量得DE=c…
【活动总结】
(1)请根据上述三种方法,依次写出A、B两点的距离.(用含字母的代数式表示)并写出方法(3)所根据的定理.
AB= ,AB=
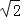 b ,AB= .
b ,AB= .定理: .
(2)请你再设计一种测量方法,(图5)画出图形,简要说明过程及结果即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)观察下列图形与等式的关系,并填空:
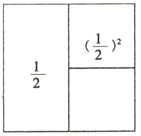
 +(
+( )2=1﹣(
)2=1﹣( )2;
)2;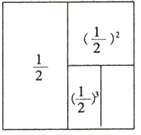
 +(
+( )2+(
)2+( )3=
)3= 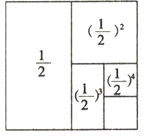
 +(
+( )2+(
)2+( )3+(
)3+( )4=
)4= (规律探究)观察下图:
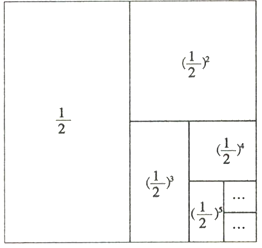
根据以上发现,用含n的代数式填空:
 +(
+( )2+(
)2+( )3+(
)3+( )4+(
)4+( )5+…+(
)5+…+( )n= .
)n= .(解决问题)根据以上发现,计算:
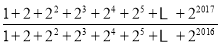 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
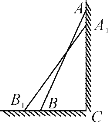
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12,
得方程___________________,解方程,得x1=____,x2=______________,∴点B将向外移动____米.
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,∠CAB=30°,∠CBA=45°,求AB的距离.(
 ≈1.41,
≈1.41,  ≈1.73,结果取整数)
≈1.73,结果取整数)
相关试题

