【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 ![]() .下列结论: ①△ADE∽△ACD;
.下列结论: ①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8或 ![]() ;
;
④CD2=CECA.
其中正确的结论是(把你认为正确结论的序号都填上)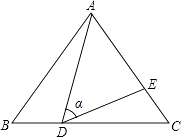
参考答案:
【答案】①②③
【解析】解:∵AB=AC, ∴∠B=∠C,
而∠ADE=∠B=α,
∴∠ADE=∠C,
而∠DAE=∠CAD,
∴△ADE∽△ACD,所以①正确;
作AH⊥BC于H,如图1,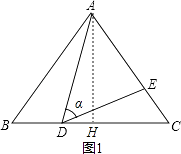
∵∠ADC=∠B+∠BAD,
∴∠BAD=∠CDE,
而∠B=∠C,
∴△ABD∽△DCE,
∵AB=AC,
∴BH=CH,
在Rt△ABH中,∵cosB=cosα= ![]() =
= ![]() ,
,
∴BH= ![]() ×10=8,
×10=8,
∴BC=2BH=16,
当BD=6时,CD=10,
∴AB=CD,
∴△ABD≌△DCE,所以②正确;
当∠DEC=90°时,
∵△ABD∽△DCE,
∴∠ADB=∠DEC=90°,即AD⊥BC,
∴点D与点H重合,此时BD=8,
当∠EDC=90°,如图2,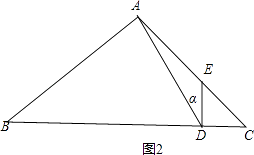
∵△ABD∽△DCE,
∴∠DAB=∠EDC=90°,
在Rt△ABD中,cosB=cosα= ![]() =
= ![]() ,
,
∴BD= ![]() =
= ![]() ,
,
∴△DCE为直角三角形时,BD为8或 ![]() ,所以③正确;
,所以③正确;
∵∠BAD=∠CDE,
而AD不是∠BAC的平分线,
∴∠CDE与∠DAC不一定相等,
∴△CDE与△CAD不一定相似,
∴CD2=CECA不成立,所以④错误.
所以答案是①②③.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由若干个(大于
 个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )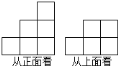
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
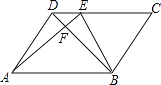
查看答案和解析>>【题目】在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,第一角限内的点A在反比例函数
 的图象上,第四象限内的点B 在反比例函数
的图象上,第四象限内的点B 在反比例函数 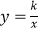 图象上,且OA⊥OB,∠OAB=60度,则k值为 .
图象上,且OA⊥OB,∠OAB=60度,则k值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B.
 ﹣1 C.
﹣1 C.  D. 2﹣
D. 2﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),
其中结论正确的个数是

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠AOC=146°,OD为∠AOC的平分线,∠AOB=90°,∠BOD的度数_____.
相关试题

