【题目】已知长方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,由
上,由![]() 往
往![]() 运动,速度为
运动,速度为![]() ,运动时间为
,运动时间为![]() 秒,将
秒,将![]() 沿着
沿着![]() 翻折至
翻折至![]() ,点
,点![]() 对应点为
对应点为![]() ,
,![]() 所在直线与边
所在直线与边![]() 交与点
交与点![]() ,
,
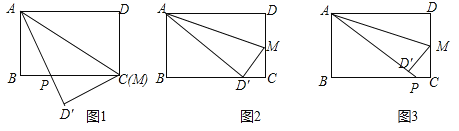
(1)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图![]() ,当
,当![]() 为何值时,点
为何值时,点![]() 恰好落在边
恰好落在边![]() 上;
上;
(3)如图![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据矩形的性质和折叠的性质可得![]() ,即可得
,即可得![]() ;
;
(2)由折叠的性质可得![]() =10cm,
=10cm,![]() ,根据勾股定理可求
,根据勾股定理可求![]() =8cm,即可得
=8cm,即可得![]() =2cm,根据勾股定理可求CM的长,即可求t的值;
=2cm,根据勾股定理可求CM的长,即可求t的值;
(3)连接MP,根据题意可得![]() ,根据“HL”可证
,根据“HL”可证![]() ≌
≌![]() ,可得
,可得![]() ,根据勾股定理可求CP的长.
,根据勾股定理可求CP的长.
证明:![]() 四边形ABCD是矩形
四边形ABCD是矩形![]()
![]() ,
,
根据折叠得,∠DAC=∠![]()
∴∠ACB=∠![]()
∴![]()
![]() 折叠
折叠
∴![]() =10cm,
=10cm,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]()
∴![]()
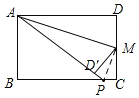
![]() 如图,连接MP,
如图,连接MP,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 折叠
折叠
∴![]() =10cm,
=10cm,![]() ,
,
∴![]() ,且
,且![]()
![]() ≌Rt△D′MP(HL)
≌Rt△D′MP(HL)
∴![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品
 件(
件( >0),购买两种商品共花费
>0),购买两种商品共花费 元.
元.(1)求出
 与
与 的函数关系式(写出自变量
的函数关系式(写出自变量 的取值范围);
的取值范围);(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2+(3m+1)x+3=0.

(1)求证:该方程有两个实数根;
(2)如果抛物线y=mx2+(3m+1)x+3与x轴交于A、B两个整数点(点A在点B左侧),且m为正整数,求此抛物线的表达式;
(3)在(2)的条件下,抛物线y=mx2+(3m+1)x+3与y轴交于点C,点B关于y轴的对称点为D,设此抛物线在﹣3≤x≤﹣ 之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围.
之间的部分为图象G,如果图象G向右平移n(n>0)个单位长度后与直线CD有公共点,求n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离
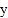 (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.(1)A,B两城相距 千米,乙车比甲车早到 小时;
(2)甲车出发多长时间与乙车相遇?
(3)若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.
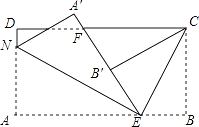
(1)若∠BEB′=110°,则∠BEC=°,∠AEN=°,∠BEC+∠AEN=°.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线l1:
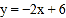 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2: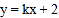 (
( ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.(1)求点A,B的坐标;
(2)如图,当
 =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与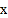 轴围成的△BDE的面积;
轴围成的△BDE的面积;(3)若直线l1,l2与
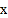 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2: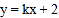 (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.①求
 的值;
的值;②若
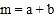 ,,求
,,求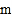 的取值范围.
的取值范围.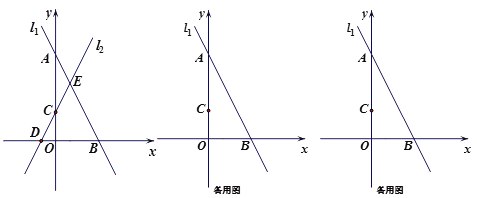
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BD是直径.若
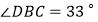 ,则
,则 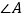 等于( )
等于( )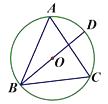
A.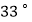

B.
C.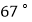
D.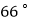
相关试题

