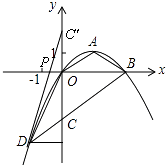
【题目】如图,顶点为A( ![]() ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
参考答案:
【答案】
(1)
解:∵抛物线顶点为A( ![]() ,1),
,1),
设抛物线解析式为y=a(x﹣ ![]() )2+1,
)2+1,
将原点坐标(0,0)在抛物线上,
∴0=a( ![]() )2+1
)2+1
∴a=﹣ ![]() .
.
∴抛物线的表达式为:y=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:令y=0,得 0=﹣ ![]() x2+
x2+ ![]() x,
x,
∴x=0(舍),或x=2 ![]()
∴B点坐标为:(2 ![]() ,0),
,0),
设直线OA的表达式为y=kx,
∵A( ![]() ,1)在直线OA上,
,1)在直线OA上,
∴ ![]() k=1,
k=1,
∴k= ![]() ,
,
∴直线OA对应的一次函数的表达式为y= ![]() x.
x.
∵BD∥AO,
设直线BD对应的一次函数的表达式为y= ![]() x+b,
x+b,
∵B(2 ![]() ,0)在直线BD上,
,0)在直线BD上,
∴0= ![]() ×2
×2 ![]() +b,
+b,
∴b=﹣2,
∴直线BD的表达式为y= ![]() x﹣2.
x﹣2.
由 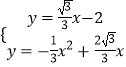
得交点D的坐标为(﹣ ![]() ,﹣3),
,﹣3),
令x=0得,y=﹣2,
∴C点的坐标为(0,﹣2),
由勾股定理,得:OA=2=OC,AB=2=CD,OB=2 ![]() =OD.
=OD.
在△OAB与△OCD中,
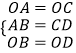 ,
,
∴△OAB≌△OCD.
(3)
解:点C关于x轴的对称点C'的坐标为(0,2),
∴C'D与x轴的交点即为点P,它使得△PCD的周长最小.
过点D作DQ⊥y,垂足为Q,
∴PO∥DQ.
∴△C'PO∽△C'DQ.
∴ ![]() ,
,
∴ ![]() ,
,
∴PO= ![]() ,
,
∴点P的坐标为(﹣ ![]() ,0)
,0)
【解析】(1)用待定系数法求出抛物线解析式,(2)先求出直线OA对应的一次函数的表达式为y= ![]() x.再求出直线BD的表达式为y=
x.再求出直线BD的表达式为y= ![]() x﹣2.最后求出交点坐标C,D即可;(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
x﹣2.最后求出交点坐标C,D即可;(3)先判断出C'D与x轴的交点即为点P,它使得△PCD的周长最小.作辅助线判断出△C'PO∽△C'DQ即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).

(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD 面上的概率为 ;若存在,指出其中的一种平移方式;若不存在,请说明理由.
;若存在,指出其中的一种平移方式;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论中正确的是( )

①△BCD为等腰三角形;②BF=AC;③CE=
 BF;④BH=CE.
BF;④BH=CE.A. ①② B. ①③ C. ①②③ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坐标平面上,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点的纵坐标都是-3,D,E两点在y轴上,则点F到y轴的距离为____.
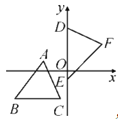
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲种节能灯
30
40
甲种节能灯
35
50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小张用 6000 元购进 A,B 两种服装,按标价售出后可获得毛利 3800元(毛利=售价﹣进价).现已知 A 种服装的进价是 60 元/件,标价是 100 元/件;B 种服装的进价是 100 元/件,标价是 160 元/件.
(1)这两种服装各购进了多少件?
(2)如果 A 种服装按标价的 8 折出售,B 种服装按标价的 7 折出售,那么这批服装全部售完后,小张比按标价出售少收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某专卖店有 A,B 两种商品.已知在打折前,买 20 件 A 商品和 10 件B 商品用了 400 元;买 30 件 A 商品和 20 件 B 商品用了 640 元.A,B 两种商品打相同折以后,某人买 100 件 A 商品和 200 件 B 商品一共比不打折少花 640 元,计算打了多少折?
相关试题

