【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论中正确的是( )

①△BCD为等腰三角形;②BF=AC;③CE=![]() BF;④BH=CE.
BF;④BH=CE.
A. ①② B. ①③ C. ①②③ D. ①②③④
参考答案:
【答案】C
【解析】
根据“等腰三角形的判定与性质和全等三角形的判定与性质”结合“已知条件”进行分析解答即可.
(1)∵CD⊥AB,
∴∠BDC=∠CDA=90°,
又∵∠ABC=45°,
∴∠BCD=45°=∠ABC,
∴BD=CD,
∴△BCD是等腰三角形,即结论①成立;
(2)∵BE⊥AC,
∴∠AEB=∠CDA=90°,
∴∠ABF+∠A=90°,∠ACD+∠A=90°,
∴∠ABF=∠ACD,
又∵∠BDF=∠CDA=90°,BD=CD,
∴△BDF≌△CDA,
∴BF=AC,即结论②成立;
(3)∵BE⊥AC,BE平分∠ABC,
∴∠BEA=∠BEC=90°,∠ABE=∠CBE,
又∵BE=BE,
∴△ABE≌△CBE,
∴CE=AE=![]() AC,
AC,
∴CE=![]() BF,即结论③成立;
BF,即结论③成立;
(4)∵BD=CD,DH⊥BC,
∴BH=![]() BC,
BC,
∵CE=![]() AC,且不能确定AC=BC成立,
AC,且不能确定AC=BC成立,
∴不能确定BH=CE成立,即结论④不一定成立.
综上所述,4个结论中成立的是①②③.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
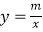 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.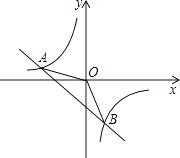
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积. -
科目: 来源: 题型:
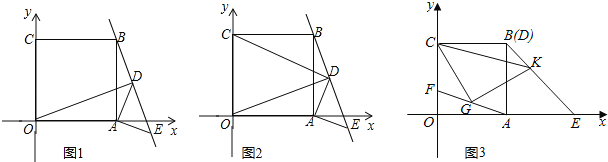
查看答案和解析>>【题目】在平面直角坐标系中,正方形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,等腰Rt△ADE的两个顶点D、E和正方形顶点B三点在一条直线上.
(1)如图1,连接OD,求证:△OAD≌△BAE;
(2)如图2,连接CD,求证:BE﹣
 DE=
DE= CD;
CD;(3)如图3,当图1中的Rt△ADE的顶点D与点B重合时,点E正好落在x轴上,F为线段OC上一动点(不与O、C重合),G为线段AF的中点,若CG⊥GK交BE于点K时,请问∠KCG的大小是否变化?若不变,请求其值;若改变,求出变化的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).

(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD 面上的概率为 ;若存在,指出其中的一种平移方式;若不存在,请说明理由.
;若存在,指出其中的一种平移方式;若不存在,请说明理由. -
科目: 来源: 题型:
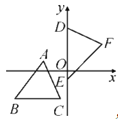
查看答案和解析>>【题目】如图,坐标平面上,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点的纵坐标都是-3,D,E两点在y轴上,则点F到y轴的距离为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为A(
 ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲种节能灯
30
40
甲种节能灯
35
50
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
相关试题

