【题目】如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标). 
(1)求P点落在正方形ABCD面上(含正方形内部和边界)的概率.
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD 面上的概率为 ![]() ;若存在,指出其中的一种平移方式;若不存在,请说明理由.
;若存在,指出其中的一种平移方式;若不存在,请说明理由.
参考答案:
【答案】
(1)解:根据题意,点P的横坐标有数字1,2,3,4四种选择,点P的纵坐标也有数字1,2,3,4四种选择,
所以构成点P的坐标共有4×4=16种情况.
如下图所示:
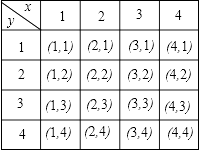
其中点P的(1,1),(1,2),(2,1),(2,2)四种情况将落在正方形ABCD面上,
故所求的概率为 ![]()
(2)解:因为要使点P落在正方形ABCD面上的概率为 ![]() ,所以只能将正方形ABCD向上或向右整数个单位平移,且使点P落在正方形面上的数目为12.
,所以只能将正方形ABCD向上或向右整数个单位平移,且使点P落在正方形面上的数目为12.
∴存在满足题设要求的平移方式:先将正方形ABCD上移2个单位,后右移1个单位(先右后上亦可);
或先将正方形ABCD上移1个单位,后右移2个单位(先右后上亦可)
【解析】(1)依题意得点P的横坐标有数字1,2,3,4四种选择,纵坐标也有数字1,2,3,4四种选择,故点P的坐标共有16种情况,有四种情况将落在正方形ABCD上,所以概率为 ![]() .(2)要使点P落在正方形面上的概率为
.(2)要使点P落在正方形面上的概率为 ![]() ,所以要将正方形移动使之符合.
,所以要将正方形移动使之符合.
-
科目: 来源: 题型:
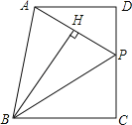
查看答案和解析>>【题目】如图,已知四边形ABCD中,AD∥BC,∠C=90°,P是CD上一点,BH⊥AP于H,BH=BC=CD
(1)求证:∠ABP=45°;
(2)若BC=20,PC=12,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数
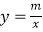 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.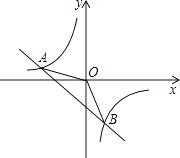
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积. -
科目: 来源: 题型:
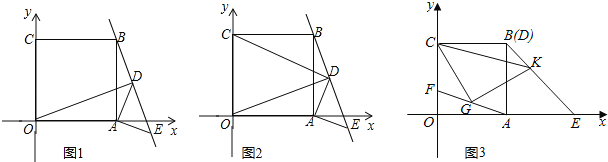
查看答案和解析>>【题目】在平面直角坐标系中,正方形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,等腰Rt△ADE的两个顶点D、E和正方形顶点B三点在一条直线上.
(1)如图1,连接OD,求证:△OAD≌△BAE;
(2)如图2,连接CD,求证:BE﹣
 DE=
DE= CD;
CD;(3)如图3,当图1中的Rt△ADE的顶点D与点B重合时,点E正好落在x轴上,F为线段OC上一动点(不与O、C重合),G为线段AF的中点,若CG⊥GK交BE于点K时,请问∠KCG的大小是否变化?若不变,请求其值;若改变,求出变化的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G,下列结论中正确的是( )

①△BCD为等腰三角形;②BF=AC;③CE=
 BF;④BH=CE.
BF;④BH=CE.A. ①② B. ①③ C. ①②③ D. ①②③④
-
科目: 来源: 题型:
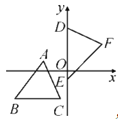
查看答案和解析>>【题目】如图,坐标平面上,△ABC≌△DEF,其中A,B,C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B,C两点的纵坐标都是-3,D,E两点在y轴上,则点F到y轴的距离为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为A(
 ,1)的抛物线经过坐标原点O,与x轴交于点B.
,1)的抛物线经过坐标原点O,与x轴交于点B.
(1)求抛物线对应的二次函数的表达式;
(2)过B作OA的平行线交y轴于点C,交抛物线于点D,求证:△OCD≌△OAB;
(3)在x轴上找一点P,使得△PCD的周长最小,求出P点的坐标.
相关试题

