【题目】如图所示,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.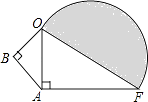
参考答案:
【答案】解:如图,∵在直角△ABO中,∠B=90°,BO=3cm,AB=4cm,
∴AO= ![]() =5cm.
=5cm.
则在直角△AFO中,由勾股定理得到:FO= ![]() =13cm,
=13cm,
∴图中半圆的面积= ![]() π×(
π×( ![]() )2=
)2= ![]() π×
π× ![]() =
= ![]() (cm2).
(cm2).
答:图中半圆的面积是 ![]() cm2 .
cm2 .
【解析】首先,在直角△ABO中,利用勾股定理求得AO=5cm;然后在直角△AFO中,由勾股定理求得斜边FO的长度;最后根据圆形的面积公式进行解答.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】就算下面各题
(1)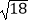 ×
× 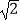 ﹣5
﹣5
(2)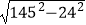
(3)(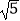 ﹣
﹣ 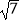 )(
)( 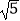 +
+ 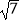 )+2
)+2
(4)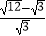 ﹣(1﹣
﹣(1﹣ 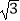 )0 .
)0 . -
科目: 来源: 题型:
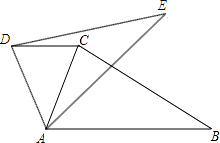
查看答案和解析>>【题目】如图,在同一平面内,将△ABC绕点A旋转到△AED的位置,若AE⊥BC,∠ADC=65°,则∠ABC的度数为( )
A.30°
B.40°
C.50°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
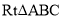 中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由。
(3)点P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式相乘的结果是a2﹣a﹣6的是( )
A.(a﹣2)(a+3)
B.(a+2)(a﹣3)
C.(a﹣6)(a+1)
D.(a+6)(a﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
-
科目: 来源: 题型:
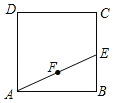
查看答案和解析>>【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
相关试题

