【题目】如图,在同一平面内,将△ABC绕点A旋转到△AED的位置,若AE⊥BC,∠ADC=65°,则∠ABC的度数为( )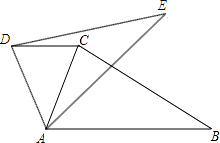
A.30°
B.40°
C.50°
D.60°
参考答案:
【答案】B
【解析】解:∵△ABC绕点A旋转到△AED的位置,
∴AD=AC,∠BAE=∠CAD,
∵AD=AC,
∴∠ACD=∠ADC=65°,
∴∠CAD=180°﹣65°﹣65°=50°,
∴∠BAE=50°,
∵AE⊥BC,
∴∠ABC=90°﹣∠BAE=40°.
故选B.
【考点精析】根据题目的已知条件,利用图形的旋转的相关知识可以得到问题的答案,需要掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
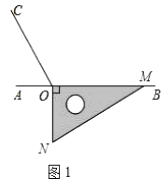
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.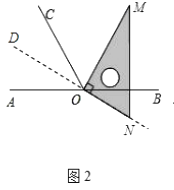
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM﹣∠NOC的度数.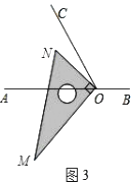
-
科目: 来源: 题型:
查看答案和解析>>【题目】就算下面各题
(1)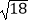 ×
× 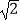 ﹣5
﹣5
(2)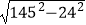
(3)(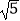 ﹣
﹣ 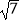 )(
)( 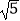 +
+ 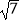 )+2
)+2
(4)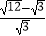 ﹣(1﹣
﹣(1﹣ 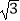 )0 .
)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
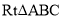 中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由。
(3)点P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.
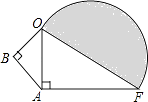
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式相乘的结果是a2﹣a﹣6的是( )
A.(a﹣2)(a+3)
B.(a+2)(a﹣3)
C.(a﹣6)(a+1)
D.(a+6)(a﹣1)
相关试题

