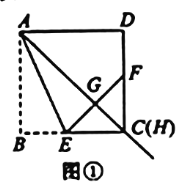
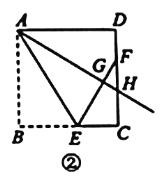
【题目】在正方形![]() 中,过点A引射线
中,过点A引射线![]() ,交边
,交边![]() 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线![]() 上的点G处,折痕
上的点G处,折痕![]() 交
交![]() 于E,连接E,G并延长
于E,连接E,G并延长![]() 交
交![]() 于F.
于F.
(1)如图1,当点H与点C重合时,![]() 与
与![]() 的大小关系是_________;
的大小关系是_________;![]() 是____________三角形.
是____________三角形.
(2)如图2,当点H为边![]() 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(3)在图2,当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;等腰直角.(2)详见解析;(3)
;等腰直角.(2)详见解析;(3)![]()
【解析】
(1)连接AF,由正方形的性质及折叠的性质已知![]() ,由全等可知
,由全等可知![]() ,CF=CE,结合
,CF=CE,结合![]() 可确定
可确定![]() 是等腰直角三角形;(2)连接AF,由正方形的性质及折叠的性质已知
是等腰直角三角形;(2)连接AF,由正方形的性质及折叠的性质已知![]() ,即证
,即证![]() ;(3)设
;(3)设![]() ,依据题意及(2)的结论用含x的式子确定出
,依据题意及(2)的结论用含x的式子确定出![]() 的三边长,根据勾股定理求出x的值,即可求面积.
的三边长,根据勾股定理求出x的值,即可求面积.
解:(1)连接![]() ,
,
∵四边形![]() 是正方形,∴
是正方形,∴![]() ,
,![]() .
.
由翻折可知![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .…
.…
∴![]() .
.
又![]() 平分
平分![]()
∴AC垂直平分EF
∴![]()
∴![]() 是等腰直角三角形.
是等腰直角三角形.
故答案为:![]() ;等腰直角.
;等腰直角.
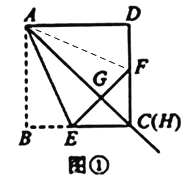
(2)连接![]() ,
,
∵四边形![]() 是正方形的对角线,∴
是正方形的对角线,∴![]() ,
,![]() .
.
由翻折可知![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .…
.…
∴![]() .…
.…
(3)设![]() ,则
,则![]() ,
,![]() .
.
在![]() 中,
中,![]() ,即
,即![]() .
.
解得![]() ,即
,即![]() 的长为
的长为![]() .
.
∴![]() ;…
;…
∴![]() .…
.…
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
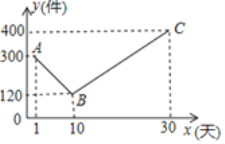
(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD交于点F,AC⊥AB于点A,点E在边CD上,且满足DFDB=DEDC,FE=FB,BD平分∠ABE,若AB=6,CF=9,则OE的长为_____.
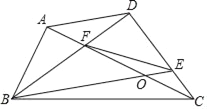
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读材料:如图(1),在数轴上
 示的数为
示的数为 ,
,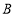 点表示的数为
点表示的数为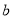 ,则点
,则点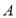 到点
到点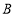 的距离记为
的距离记为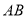 .线段
.线段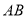 的长可以用右边的数减去左边的数表示,即
的长可以用右边的数减去左边的数表示,即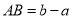 .
.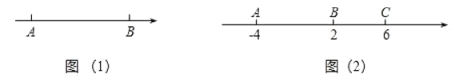
解决问题:如图(2),数轴上点
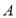 表示的数是-4,点
表示的数是-4,点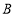 表示的数是2,点
表示的数是2,点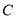 表示的数是6.
表示的数是6.(1)若数轴上有一点
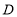 ,且
,且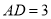 ,则点
,则点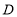 表示的数为 ;
表示的数为 ;(2)点
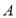 、
、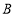 、
、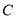 开始在数轴上运动,若点
开始在数轴上运动,若点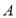 以每秒1个单位长度的速度向左运动,同时,若点
以每秒1个单位长度的速度向左运动,同时,若点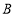 和点
和点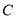 分别以每秒2个单位长度和3个单位长度的速度向右运动,假设
分别以每秒2个单位长度和3个单位长度的速度向右运动,假设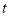 秒钟过后,若点
秒钟过后,若点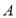 与点
与点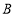 之间的距离表示为
之间的距离表示为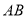 ,点
,点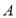 与点
与点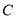 之间的距离表示为
之间的距离表示为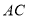 ,点
,点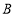 与点
与点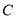 之间的距离表示为
之间的距离表示为 .则点
.则点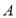 表示的数是 (用含
表示的数是 (用含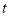 的代数式表示),
的代数式表示),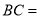 (用含
(用含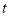 的代数式表示).
的代数式表示).(3)请问:
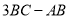 的值是否随着时间
的值是否随着时间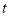 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,添加下列条件仍然不能使ABCD成为菱形的是( )
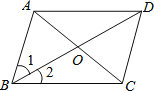
A. AB=BC B. AC⊥BD C. ∠ABC=90° D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
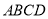 外取一点
外取一点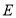 ,连接
,连接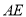 、
、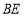 、
、 .过点
.过点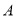 作
作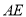 的垂线交
的垂线交 于点
于点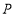 ,连接
,连接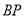 .若
.若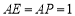 ,
,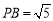 ,下列结论:①
,下列结论:①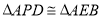 ;②
;②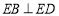 ;③点
;③点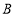 到直线
到直线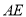 的距离为
的距离为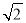 ;④
;④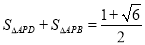 ,其中正确的结论有_____________(填序号)
,其中正确的结论有_____________(填序号)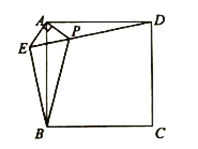
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正方形ABCD外切于⊙O,切点分别为E、F、G、H.则图中阴影部分的面积为______.

相关试题

