搜索
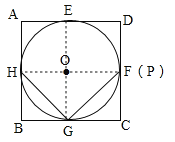
【题目】如图，边长为4的正方形ABCD外切于⊙O，切点分别为E、F、G、H．则图中阴影部分的面积为______．
参考答案：
【答案】2π+4．
【解析】解：如图，连接HO，延长HO交CD于点P，∵正方形ABCD外切于⊙O，∴∠A=∠D=∠AHP=90°，∴四边形AHPD为矩形，∴∠OPD=90°，又∠OFD=90°，∴点P于点F重合，则HF为⊙O的直径，同理EG为⊙O的直径，由∠B=∠OGB=∠OHB=90°且OH=OG知，四边形BGOH为正方形，同理四边形OGCF、四边形OFDE、四边形OEAH均为正方形，∴BH=BG=GC=CF=2，∠HGO=∠FGO=45°，∴∠HGF=90°，GH=GF=
=
，则阴影部分面积=
S⊙O+S△HGF=
π22+
×
×
=2π+4．故答案为：2π+4．
-
科目： 来源： 题型：
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发，先向西骑行2km到达A村，继续向西骑行3km到达B村，然后向东骑行9km到达C村，最后回到邮局．
（1）以邮局为原点，向东方向为正方向，用1cm表示1km，画出数轴，并在该数轴上表示A、B、C三个村庄的位置；
（2）C村离A村有多远？
（3）若摩托车的油耗为每千米0.03L，求邮递员这次出行的耗油量．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，直线a 、b被直线c所截，现给出下列四种条件：
①∠2＝∠6 ②∠2＝∠8 ③∠1＋∠4＝180° ④∠3＝∠8，其中能判断是a∥b的条件的序号是（ ）
A. ①② B. ①③ C. ①④ D. ③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正六边形ABCDEF的边长为
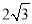，延长BA，EF交于点O.以O为原点，以边AB所在的直线为
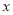轴建立平面直角坐标系，则直线DF与直线AE的交点坐标是(_______).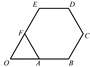
-
科目： 来源： 题型：
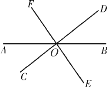
查看答案和解析>>【题目】如图，直线AB，CD，EF相交于点O，则∠AOD的对顶角是_________，∠AOC的邻补角是_______．若∠AOC＝50°，则∠BOD＝__________，∠COB＝______________．
-
科目： 来源： 题型：
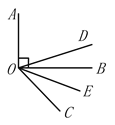
查看答案和解析>>【题目】如图，DO平分∠AOC，OE平分∠BOC，若OA⊥OB，
（1）当∠BOC＝30°，∠DOE＝_______________； 当∠BOC＝60°，∠DOE＝_______________；
（2）通过上面的计算，猜想∠DOE的度数与∠AOB有什么关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】九(1)班数学兴趣小组经过市场调查，整理出某种商品在第x(
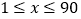)天的售价与销量的相关信息如下表：时间(天)
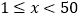
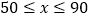
售价(元/件)
x+40
90
每天销量(件)
200-2x
200-2x
(1)求出y与x的函数关系式；
(2)问销售该商品第几天时，当天销售利润最大？最大利润是多少？
(3)该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.
相关试题
