【题目】先阅读材料:如图(1),在数轴上![]() 示的数为
示的数为![]() ,
,![]() 点表示的数为
点表示的数为![]() ,则点
,则点![]() 到点
到点![]() 的距离记为
的距离记为![]() .线段
.线段![]() 的长可以用右边的数减去左边的数表示,即
的长可以用右边的数减去左边的数表示,即![]() .
.
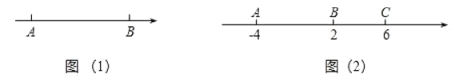
解决问题:如图(2),数轴上点![]() 表示的数是-4,点
表示的数是-4,点![]() 表示的数是2,点
表示的数是2,点![]() 表示的数是6.
表示的数是6.
(1)若数轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 表示的数为 ;
表示的数为 ;
(2)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,若点
以每秒1个单位长度的速度向左运动,同时,若点![]() 和点
和点![]() 分别以每秒2个单位长度和3个单位长度的速度向右运动,假设
分别以每秒2个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .则点
.则点![]() 表示的数是 (用含
表示的数是 (用含![]() 的代数式表示),
的代数式表示),![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
(3)请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
参考答案:
【答案】(1)-7或-1;(2)![]() ,
,![]() ;(3)不变,值为6.
;(3)不变,值为6.
【解析】
(1)设点D表示的数为d,于是得到|﹣4﹣d|=3,求得d=﹣1或﹣7,于是得到结论;
(2)利用题意结合数轴表示出A、B、C三点表示的数,进而可得结论;
(3)根据题意列式计算即可得到结论.
(1)设点D表示的数为d.
∵点A表示的数是﹣4,AD=3,∴|﹣4﹣d|=3,
解得:d=﹣1或﹣7,∴点D表示的数为﹣7或﹣1.
故答案为:﹣7或﹣1;
(2)点A表示的数是﹣4﹣t,点B表示的数是2t+2,点C表示的数是3t+6,∴BC=(3t+6)﹣(2t+2)=t+4.
故答案为:﹣4﹣t,t+4;
(3)不变,值为6.理由如下:
AB=(2t+2)﹣(﹣4﹣t)=2t+2+4+t=3t+6
3BC﹣AB=3(t+4)﹣(3t+6)
=3t+12﹣3t﹣6,
=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在把一张正方形纸片按如图方式剪去一个半径为40
 厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米,
厘米的圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米.(不计损耗、重叠,结果精确到1厘米, ≈1.41,
≈1.41,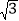 ≈1.73)
≈1.73)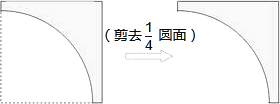
A. 64 B. 67 C. 70 D. 73
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
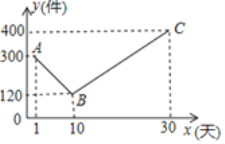
(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD交于点F,AC⊥AB于点A,点E在边CD上,且满足DFDB=DEDC,FE=FB,BD平分∠ABE,若AB=6,CF=9,则OE的长为_____.
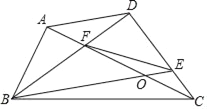
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形
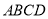 中,过点A引射线
中,过点A引射线 ,交边
,交边 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线 上的点G处,折痕
上的点G处,折痕 交
交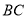 于E,连接E,G并延长
于E,连接E,G并延长 交
交 于F.
于F.(1)如图1,当点H与点C重合时,
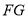 与
与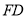 的大小关系是_________;
的大小关系是_________;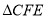 是____________三角形.
是____________三角形.(2)如图2,当点H为边
 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接 ,猜想
,猜想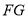 与
与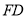 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.(3)在图2,当
 ,
,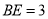 时,求
时,求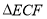 的面积.
的面积.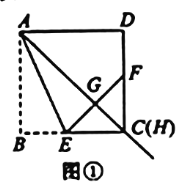
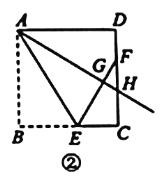
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,添加下列条件仍然不能使ABCD成为菱形的是( )
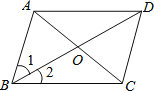
A. AB=BC B. AC⊥BD C. ∠ABC=90° D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
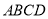 外取一点
外取一点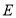 ,连接
,连接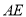 、
、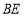 、
、 .过点
.过点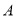 作
作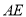 的垂线交
的垂线交 于点
于点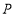 ,连接
,连接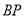 .若
.若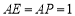 ,
,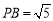 ,下列结论:①
,下列结论:①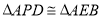 ;②
;②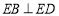 ;③点
;③点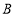 到直线
到直线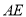 的距离为
的距离为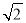 ;④
;④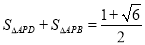 ,其中正确的结论有_____________(填序号)
,其中正确的结论有_____________(填序号)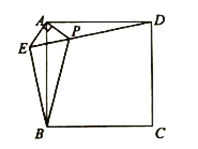
相关试题

