【题目】如图,在矩形ABCD中,点O为对角线AC、BD的交点,点E为BC上一点,连接EO,并延长交AD于点F,则图中全等三角形共有( ) 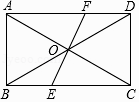
A.5对
B.6对
C.8对
D.10对
参考答案:
【答案】D
【解析】解:∵四边形ABCD为矩形,其矩形的对角线相等且相互平分, ∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
易证△ABC≌△DCB,△ABC≌△CDA,△ABC≌△BAD,△BCD≌△ADC,△BCD≌△DAB,△ADC≌△DAB,△AOF≌△COE,△DOF≌△BOE,△DOC≌△AOB,△AOD≌△BOC故图中的全等三角形共有10对.
故选D.
根据已知及全等三角形的判定方法进行分析,从而得到答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,李老师出示了如下框中的题目.
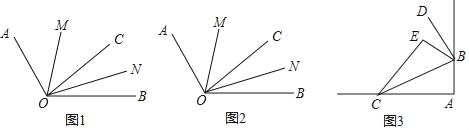
如图1,在∠AOB的内部有一条射线OC把∠AOB分成两个角,射线OM、ON分别平分∠AOC、∠BOC,试探究∠MON与∠AOB之间的数量关系,并说明理由.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论:
①请你在下表中填上当∠AOB为60°、90°、120°时∠MON的大小:
∠AOB的度数
60°
90°
120°
∠MON的度数
②探索发现:无论∠AOB的度数是多少,∠MON与∠AOB的数量关系是不变的,请你直接写出结论:
∠MON ∠AOB.
(2)特例启发,解答题目:
如图2,如果∠AOB=α,请你求∠MON的大小(用α表示).
(3)拓展结论,设计新题:
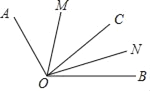
如图3,把一张报纸的一角斜折过去,使A点落在E点处,BC为折痕,BD是∠EBM的平分线,求∠CBD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图,解答下列问题.
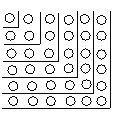
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,……,第六层有11个圆圈.如果要你继续
下去,那么第七层有几个小圆圈?第n层呢?
(2)某一层上有77个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1 + 3 = 22.
同样,
由前三层的圆圈个数和得:1 + 3 + 5 = 32.
由前四层的圆圈个数和得:1 + 3 + 5 + 7 = 42.
由前五层的圆圈个数和得:1 + 3 + 5 + 7 + 9 = 52.
……
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1 + 3 + 5 + … + 19的和;
(5)计算:11 + 13 + 15 + … + 99的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A.
B.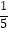
C.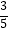
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
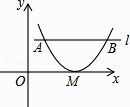
A.
B.
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S=
 .
.得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
相关试题

