搜索
【题目】如图，△ABC中，AB=AC，点D、E分别在AB、AC上，要得到△ABE≌△ACD，可添加条件（ ）
A. ∠A=∠AB. ∠ABC=∠ACBC. BE=CDD. AD=AE
参考答案：
【答案】D
【解析】
据全等三角形的判定方法：SSS、SAS、ASA、AAS、HL依次对各选项分析判断即可．
A. 由AB=AC，∠A=∠A不能得到△ABE≌△ACD，故不符合题意；
B. 由∠A=∠A，∠ABC=∠ACB，AB=AC不能得到△ABE≌△ACD，故不符合题意；
C. 由BE=CD，AB=AC, ∠A=∠A不能得到△ABE≌△ACD，故不符合题意；
D. 由AB=AC，∠A=∠A，AD=AE，根据“SAS” 能得到△ABE≌△ACD，故符合题意.
故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(a，0)，B（b，0），C(-1，2)，且
+(a+2b-4)2=0.（1）求a，b的值.
（2）在y轴的正半轴上存在一点M，使S△COM=
S△ABC，求出点M的坐标.（3）在坐标轴的其他位置是否有在点M，使S△COM=
S△ABC仍成立？若存在，请直 接写出符合条件的点M的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小东根据学习一次函数的经验，对函数y=|2x﹣1|的图象和性质进行了探究．下面是小东的探究过程，请补充完成：
（1）函数y=|2x﹣1|的自变量x的取值范围是 ；
（2）已知：
①当x=
时，y=|2x﹣1|=0； ②当x＞
时，y=|2x﹣1|=2x﹣1③当x＜
时，y=|2x﹣1|=1﹣2x；显然，②和③均为某个一次函数的一部分．
（3）由（2）的分析，取5个点可画出此函数的图象，请你帮小东确定下表中第5个点的坐标（m，n），其中m= ；n= ；：
x
…
﹣2
0
1
m
…
y
…
5
1
0
1
n
…
（4）在平面直角坐标系xOy中，作出函数y=|2x﹣1|的图象；
（5）根据函数的图象，写出函数y=|2x﹣1|的一条性质．
-
科目： 来源： 题型：
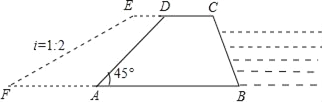
查看答案和解析>>【题目】如图，广安市防洪指挥部发现渠江边一处长400米，高8米，背水坡的坡角为45°的防洪大堤（横截面为梯形ABCD）急需加固．经调查论证，防洪指挥部专家组制定的加固方案是：背水坡面用土石进行加固，并使上底加宽2米，加固后，背水坡EF的坡比i=1：2．
（1）求加固后坝底增加的宽度AF的长；
（2）求完成这项工程需要土石多少立方米？
-
科目： 来源： 题型：
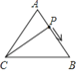
查看答案和解析>>【题目】如图，点P是等边△ABC的边上的一个做匀速运动的动点，其由点A开始沿AB边运动到B再沿BC边运动到C为止，设运动时间为t，△ACP的面积为S，则S与t的大致图象是（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．
（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；
（2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是把图1放入长方形内得到的，
，AB=3，AC=4，点D，E，F，G，H，I都在长方形KLMJ的边上，则长方形KLMJ的面积为___．
相关试题
