搜索
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).
(1) 上述操作能验证的等式是__________________;
(2) 应用你从(1)得出的等式，完成下列各题：
①已知x24y2=12，x+2y=4，求x2y的值.
②计算：(1
)(1
)(1
)…(1
)(1
).
参考答案：
【答案】（1）a2-b2=（a+b）（a-b）；（2）x-2y=3；（3）
【解析】
（1）根据两个图形中阴影部分的面积相等，即可列出等式；
（2）①把x2-4y2利用（1）的结论写成两个式子相乘的形式，然后把x+2y=4代入即可求解；
②利用（1）的结论化成式子相乘的形式即可求解．
解：（1）第一个图形中阴影部分的面积是a2-b2，第二个图形的面积是（a+b）（a-b），
则a2-b2=（a+b）（a-b）．
故答案是a2-b2=（a+b）（a-b）；
（2）①∵x2-4y2=（x+2y）（x-2y），
∴12=4（x-2y）
得：x-2y=3；
②原式=（1-
）（1+）（1-
）（1+）（1-
）（1+）…（1-
）（1+）（1-
）（1+）=
==
=.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,已知∠BDG+∠EFG=180°,∠DEF=∠B,试判断∠AED与∠C的大小关系,并加以说明.
解:∠AED=∠C.
理由:∵∠EFD+∠EFG=180°( ),
∠BDG+∠EFG=180°(已知)
∴∠BDG =∠EFD ( ),
∴BD∥EF( ),
∴∠BDE+∠DEF =180°( ).
又∵∠DEF=∠B( ),
∴∠BDE+∠B =180°( ),
∴DE∥BC( ),
∴∠AED=∠C( ).
-
科目： 来源： 题型：
查看答案和解析>>【题目】李大爷按每千克2.1元批发了一批黄瓜到镇上出售，为了方便，他带了一些零钱备用．他先按市场售出一些后，又降低出售．售出黄瓜千克数x与他手中持有的钱数y元（含备用零钱）的关系如图所示，结合图象回答下列问题：
（1）李大爷自带的零钱是多少？
（2）降价前他每千克黄瓜出售的价格是多少？
（3）卖了几天，黄瓜卖相不好了，随后他按每千克下降1.6元将剩余的黄瓜售完，这时他手中的钱（含备用的钱）是530元，问他一共批发了多少千克的黄瓜？
（4）请问李大爷亏了还是赚了？若亏（赚）了，亏（赚）多少钱？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，射线AB∥CD，P为一动点，∠BAP与∠DCP的平分线AE与CE交于点E.
(1)当P在线段AC上运动时（如图1）,即∠APC=180,则∠AEC＝______；
(2)当P运动到图2的位置时，猜想∠AEC与∠APC 的关系，并说明理由；
(3)当P运动到图3的位置时,（2）中的结论还成立吗?(不要求说明理由)
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a＞b，则下列各式中正确的是（ ）
A. a-c＜b-cB. ac＞bcC. -
（c≠0）D. a（c2+1）＞b（c2+1） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A(－4，n)、B(3，4)是一次函数y1＝kx＋b的图象与反比例函数
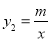的图象的两个交点，过点D(t，0)（0＜t＜3）作x轴的垂线，分别交双曲线
和直线y1＝kx＋b于P、Q两点(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时，S△BPQ＝
S△APQ(3) 以PQ为边在直线PQ的右侧作正方形PQMN，试说明：边QM与双曲线
（x＞0）始终有交点
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后，在地面上形成阴影．已知桌面的直径为1．2 m，桌面距离地面1 m．若灯泡距离地面3 m，则地面上阴影部分的面积为 ( )
A. 0．36πm2 B. 0．81πm2 C. 2πm2 D. 3.24πm2
相关试题
