【题目】如图，已知A(－4，n)、B(3，4)是一次函数y1＝kx＋b的图象与反比例函数的图象的两个交点，过点D(t，0)（0＜t＜3）作x轴的垂线，分别交双曲线和直线y1＝kx＋b于P、Q两点

(1) 直接写出反比例函数和一次函数的解析式

(2) 当t为何值时，S△BPQ＝S△APQ

(3) 以PQ为边在直线PQ的右侧作正方形PQMN，试说明：边QM与双曲线（x＞0）始终有交点

参考答案：

【答案】（1）；（2）；（3）见解析

【解析】试题分析：（1）根据点B的坐标求得反比例函数解析式，再根据反比例函数求得点A的坐标，最后根据待定系数法求得一次函数解析式即可；
（2）△APQ与△BPQ有一条公共边，根据同底的三角形的面积之比等于高之比，列出关于t的方程进行求解；
（3）设直线QM与双曲线交于C点，根据点P、Q、C三点的坐标，用t的代数式表示出QM-QC，再根据t的取值范围判断代数式的值的符号即可．

试题解析：

（1）将B（3，4）代入，得m=3×4=12，

∴反比例函数解析式为，

将A（﹣4，n）代入反比例函数，得n=﹣3，

∴A（﹣4，﹣3）

∵直线y1=kx+b过点A和点B，

∴，解得，

∴一次函数的解析式为y=x+1；

（2）如图1，∵PQ⊥x轴，

∴以PQ为底边时，△APQ与△BPQ的面积之比等于PQ边上的高之比，

又∵，

∴，

∵点D（t，0），A（﹣4，﹣3），B（3，4），

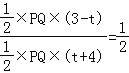∴，即，

解得；

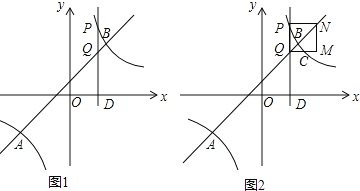
（3）如图2，设直线QM与双曲线交于C点．

依题意可知：P（t，），Q（t，t+1），C（，t+1），

∴QM=PQ=，QC=，

∴QM﹣QC==，

∵0＜t＜3，

∴0＜t（t+1）＜12，

∴＞1，

即QM﹣QC＞0，

∴QM＞QC，

即边QM与双曲线始终有交点．

关闭