【题目】如图,在△ABC中,AB=AC,过点B作BD⊥AC,垂足为D,若D是边AC的中点,
(1)求证:△ABC是等边三角形;
(2)在线段BD上求作点E,使得CE=2DE(要求:尺规作图,不写画法,保留作图痕迹)

参考答案:
【答案】(1)答案见详解;(2)答案见详解.
【解析】
(1)先证BD垂直平分AC,得到BC=AB,再由AB=AC证得三边相等,由此证得结论;
(2)根据CE=2DE分析得到CE平分∠ACB,依此画图即可.
(1)∵BD⊥AC,D是边AC的中点,
∴BD垂直平分AC,
∴BC=AB,
∵AB=AC,
∴AB=AC=BC,
∴△ABC是等边三角形;
(2)∵CE=2DE, BD⊥AC,
∴∠DCE=30![]() ,
,
∵∠ACB=60![]() ,
,
∴CE平分∠ACB.
依此画图如下:
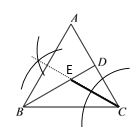
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种单价为
 元的篮球,如果以单价
元的篮球,如果以单价 元出售,那么每月可售出
元出售,那么每月可售出 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高 元,销售量相应减少
元,销售量相应减少 个;
个;某商场购进一种单价为
 元的篮球,如果以单价
元的篮球,如果以单价 元出售,那么每月可售出
元出售,那么每月可售出 个,根据销售经验,售价每提高
个,根据销售经验,售价每提高 元,销售量相应减少
元,销售量相应减少 个;
个; 假设销售单价提高
假设销售单价提高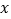 元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含
元,那么销售每个篮球所获得的利润是________元;这种篮球每月的销售量是________个;(用含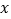 的代数式表示)
的代数式表示) 若商店准备获利
若商店准备获利 元,则销售定价为多少元?商店应进货多少个?
元,则销售定价为多少元?商店应进货多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
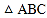 中,
中,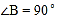 ,
,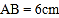 ,
,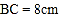 .
.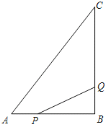
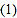 点
点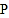 从点
从点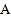 开始沿
开始沿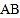 边向
边向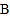 以
以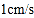 的速度移动,点
的速度移动,点 从
从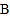 点开始沿
点开始沿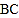 边向点
边向点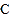 以
以 的速度移动.如果
的速度移动.如果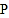 、
、 分别从
分别从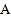 ,
,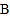 同时出发,线段
同时出发,线段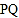 能否将
能否将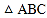 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由. 若
若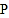 点沿射线
点沿射线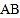 方向从
方向从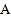 点出发以
点出发以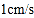 的速度移动,点
的速度移动,点 沿射线
沿射线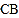 方向从
方向从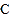 点出发以
点出发以 的速度移动,
的速度移动,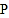 、
、 同时出发,问几秒后,
同时出发,问几秒后,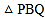 的面积为
的面积为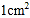 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥
的图象上,PC⊥ 轴于点C,交
轴于点C,交 的图象于点A,PC⊥
的图象于点A,PC⊥ 轴于点D,交
轴于点D,交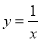 的图象于点B. 当点P在
的图象于点B. 当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:①

②
 的值不会发生变化
的值不会发生变化③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业在甲地有一工厂(简称甲厂)生产某产品,2017年的年产量过万件,2018年甲厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件.
(1)若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?
(2)由于该产品深受顾客欢迎,2019年该企业在乙地建立新厂(简称乙厂)生产该产品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m,n件产品(甲厂的日均产量与2018年相同),m:n=14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△PQN中,若∠P=
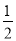 ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
相关试题

