【题目】某企业在甲地有一工厂(简称甲厂)生产某产品,2017年的年产量过万件,2018年甲厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件.
(1)若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?
(2)由于该产品深受顾客欢迎,2019年该企业在乙地建立新厂(简称乙厂)生产该产品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m,n件产品(甲厂的日均产量与2018年相同),m:n=14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.
参考答案:
【答案】(1)99件;(2)甲厂先完成任务,理由见详解.
【解析】
(1)设2017年甲厂日均生产该产品x件,根据2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同列得方程;
(2)先求出甲、乙两厂的日均生产数量,用含m的代数式表示n,再分别表示出甲、乙两厂的生产时间,进行比较即可得到答案.
(1)设2017年甲厂日均生产该产品x件,则2018年甲厂日均生产该产品(2x+2)件,
![]() ,
,
x=99,
经检验,x=99是原分式方程的解,
答:2017年甲厂日均生产该产品99件.
(2)2019年甲厂日均生产![]() 件,乙厂日均生产
件,乙厂日均生产![]() 件,
件,
∵m:n=14:25,
∴![]() ,
,
∴甲厂生产m个所需要的时间为: 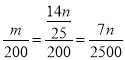 ,
,
乙厂生产n个所需要的时间为:![]()
∵![]() ,
,
∴甲厂先完成任务.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?请完成下列问题:
(1)未降价之前,某商场衬衫的总盈利为 元.
(2)降价后,设某商场每件衬衫应降价x元,则每件衬衫盈利 元,平均每天可售出 件(用含x的代数式进行表示)
(3)请列出方程,求出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,过点B作BD⊥AC,垂足为D,若D是边AC的中点,
(1)求证:△ABC是等边三角形;
(2)在线段BD上求作点E,使得CE=2DE(要求:尺规作图,不写画法,保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥
的图象上,PC⊥ 轴于点C,交
轴于点C,交 的图象于点A,PC⊥
的图象于点A,PC⊥ 轴于点D,交
轴于点D,交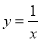 的图象于点B. 当点P在
的图象于点B. 当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:①

②
 的值不会发生变化
的值不会发生变化③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△PQN中,若∠P=
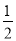 ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=
 (x>0)的图象经过顶点B,则反比例函数的表达式为( )
(x>0)的图象经过顶点B,则反比例函数的表达式为( )
A. y=
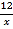 B. y=
B. y=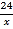 C. y=
C. y=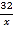 D. y=
D. y=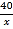
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.

(1)概念理解:
如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求
 的值.
的值.(3)应用拓展:
如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的
 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
相关试题

