【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
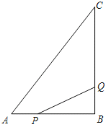
![]() 点
点![]() 从点
从点![]() 开始沿
开始沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() ,
,![]() 同时出发,线段
同时出发,线段![]() 能否将
能否将![]() 分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
![]() 若
若![]() 点沿射线
点沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,点
的速度移动,点![]() 沿射线
沿射线![]() 方向从
方向从![]() 点出发以
点出发以![]() 的速度移动,
的速度移动,![]() 、
、![]() 同时出发,问几秒后,
同时出发,问几秒后,![]() 的面积为
的面积为![]() ?
?
参考答案:
【答案】(1) 线段![]() 不能将
不能将![]() 分成面积相等的两部分;(2) 经过
分成面积相等的两部分;(2) 经过![]() 秒、
秒、![]() 秒或
秒或![]() 秒后,
秒后,![]() 的面积为
的面积为![]() .
.
【解析】
(1)设经过x秒,线段PQ能否将△ABC分成面积相等的两部分,根据面积之间的等量关系和判别式即可求解;
(2)分三种情况:①点P在线段AB上,点Q在线段CB上(0<t≤4);②点P在线段AB上,点Q在线段CB上(4<t≤6);③点P在射线AB上,点Q在射线CB上(t>6);进行讨论即可求解.
(1)设经过x秒,线段PQ能将△ABC分成面积相等的两部分
由题意知:AP=x,BQ=2x,则BP=6﹣x,∴![]() (6﹣x)2x=
(6﹣x)2x=![]() ×
×![]() ×6×8,∴x2﹣6x+12=0.
×6×8,∴x2﹣6x+12=0.
∵b2﹣4ac<0,此方程无解,∴线段PQ不能将△ABC分成面积相等的两部分;
(2)设t秒后,△PBQ的面积为1.分三种情况讨论:
①当点P在线段AB上,点Q在线段CB上时,此时0<t≤4.
由题意知:![]() (6﹣t)(8﹣2t)=1,整理得:t2﹣10t+23=0,解得:t1=5+
(6﹣t)(8﹣2t)=1,整理得:t2﹣10t+23=0,解得:t1=5+![]() (不合题意,应舍去),t2=5﹣
(不合题意,应舍去),t2=5﹣![]()
②当点P在线段AB上,点Q在线段CB的延长线上时,此时4<t≤6,由题意知:![]() (6﹣t)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=t2=5.
(6﹣t)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=t2=5.
③当点P在线段AB的延长线上,点Q在线段CB的延长线上时![]() (t﹣6)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=5+
(t﹣6)(2t﹣8)=1,整理得:t2﹣10t+25=0,解得:t1=5+![]() ,t2=5﹣
,t2=5﹣![]() (不合题意,应舍去).
(不合题意,应舍去).
综上所述:经过5﹣![]() 秒、5秒或5+
秒、5秒或5+![]() 秒后,△PBQ的面积为1.
秒后,△PBQ的面积为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是李刚同学在一次测验中解答的数学题:
①若
 ,则
,则 ,
,②方程
 的解为
的解为 ,
,③若
 两根的倒数和等于
两根的倒数和等于 ,则
,则 ,
,④若
 是方程
是方程 的解,则
的解,则 或
或 .
.其中答对的是________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,点 D,E 分别在∠ABC 和∠ACB 的平分线上,连接 BD,DE,EC,若∠D+∠E=295°, 则∠A 是( )
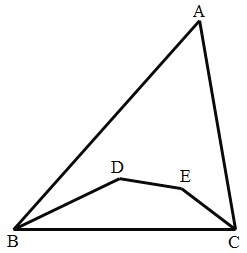
A.65°B.60°C.55°D.50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 A,B,C 的坐标分别是(2,1),(6,1),(3,5),若△A1B1C1 与△ABC 关于x 轴对称
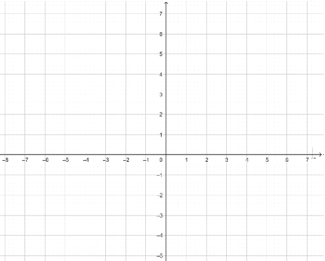
(1)在平面直角坐标系中画出△A1B1C1,并写出 A1,B1,C1 三个点的坐标
(2)求出△A1B1C1的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的方程
的方程 有实数根,则
有实数根,则 满足________.
满足________. -
科目: 来源: 题型:
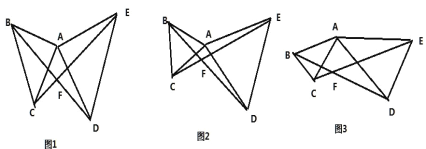
查看答案和解析>>【题目】(1)如图 1,△ABC 和△ADE 都是等腰直角三角形,∠BAC 和∠DAE 是直角,连接BD,CE 相交于点 F,则∠BFC= °
(2)如图 2,△ABC 和△ADE 都是等边三角形,连接 BD,CE 相交于点 F,则∠BFC= °
(3)如图 3,△ABC 和△ADE 都是等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE,连接 BD,CE相交于点 F,请猜想∠BFC 与∠BAC 有怎样的大小关系?请证明你的猜想
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD

(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
相关试题

