【题目】解答
(1)如图①,等边△ABC中,点D是AB边上的一动点(点D与点B不重合),以CD为一边,向上作等边△EDC,连接AE.你能发现线段AE、AD与AC之间的数量关系吗?证明你发现的结论. 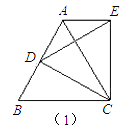
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想线段AE、AD与AC之间的数量关系,并说明理由. 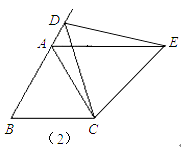
参考答案:
【答案】
(1)解:结论:AC=AD+AE,
证明如下:
∵△ABC、△CDE为等边三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
∴∠ECA+∠ACD=∠ACD+∠BCD,
∴∠ECA=∠BCD,
在△ACE和△BCD中
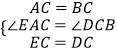
∴△ACE≌△BCD(SAS),
∴AE=BD,
∴AC=AB=AD+BD=AD+AE
(2)解:结论:AC=AE﹣AD,
理由如下:
同(1)可证明△ACE≌△BCD,
∴AE=BD,
∴AC=AB=BD﹣AD=AE﹣AD
【解析】(1)利用条件可证明△ACE≌△BCD,则可得到AE=BE,再利用线段的和差可证得结论AC=AD+AE;(2)由条件可证明△ACE≌△BCD,同样可以得到结论AC=AE﹣AD.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一角顶点B在y轴上.
(1)如图①若AD⊥x轴,垂足为点D.点C坐标是(﹣1,0),点B的坐标是(0,2),求A点的坐标.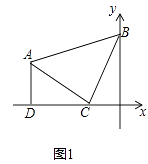
(2)如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,求证:BD=2AE.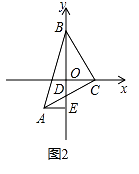
(3)如图③,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论:①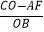 为定值;②
为定值;② 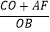 为定值,只有一个结论成立,请你判断正确的结论并求出定值.
为定值,只有一个结论成立,请你判断正确的结论并求出定值.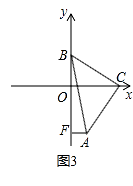
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣(x﹣2)2﹣3的顶点坐标是( )
A.(﹣2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器专卖店策划五一促销活动,已知一款电视机的成本价为1800元/台,专卖店计划将其打七五折销售,同时还要保证每台至少获得10%的利润.若设该款电视机的标价为x元/台,则x满足的不等关系为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(﹣3,1)关于原点对称的点的坐标是( )
A.(1,3)
B.(3,﹣1)
C.(﹣3,﹣1)
D.(﹣1,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】设a、b是一元二次方程x2﹣2x﹣1=0的两个根,则a2+a+3b的值为____.
-
科目: 来源: 题型:
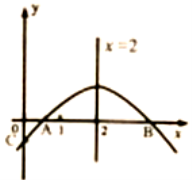
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c (a≠0)的图像与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC. 则下列结论:
①abc>0 ②9a+3b+c<0 ③c>-1 ④关于x的方程ax2+bx+c=0 (a≠0)有一个根为-
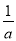
其中正确的结论个数有( )
A. 1个 B. 2个 C.3个 D. 4个
相关试题

