【题目】△ABC是等腰直角三角形,BC=AC,直角顶点C在x轴上,一角顶点B在y轴上.
(1)如图①若AD⊥x轴,垂足为点D.点C坐标是(﹣1,0),点B的坐标是(0,2),求A点的坐标.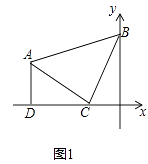
(2)如图②,直角边BC在两坐标轴上滑动,若y轴恰好平分∠ABC,AC与y轴交于点D,过点A作AE⊥y轴于E,求证:BD=2AE.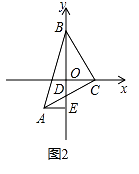
(3)如图③,直角边BC在两坐标轴上滑动,使点A在第四象限内,过A点作AF⊥y轴于F,在滑动的过程中,两个结论:① ![]() 为定值;②
为定值;② ![]() 为定值,只有一个结论成立,请你判断正确的结论并求出定值.
为定值,只有一个结论成立,请你判断正确的结论并求出定值.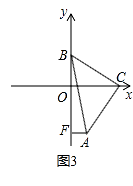
参考答案:
【答案】
(1)
解:∵∠ACB=90°,
∴∠ACD+∠BCO=90°,
∵AD⊥CD,
∴∠ACD+∠CAD=90°,
∴∠BCO=∠CAD,
在△ACD和△CBO中, 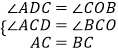 ,
,
∴△ACD≌△CBO,
∴AD=CO=1,DC=OB=2,
∴OD=OC+CD=3,
∴A(﹣3,1)
(2)
解:如图,
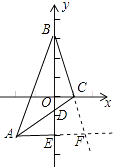
延长AE、BC交于点F,
∵y轴平分∠ABC,AE⊥y轴,
∴AE=EF,
∴AF=2AE,
∵AE⊥x轴,
∴∠EAD+∠ADE=90°,
∵∠ADE=∠BDC,
∴∠EAD+∠BDC=90°,
∵∠ABC=90°,
∴∠BDC+∠CBD=90°,
∴∠DAE=∠CBD,
在△BCD和△ACF中, 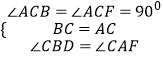 ,
,
∴△BCD≌△ACF,
∴BD=AF,
∵AF=2AE,
∴BD=2AE
(3)
解:① ![]() 为定值,理由:
为定值,理由:
如图3,
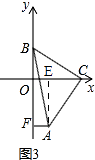
作AE⊥OC于E,
∵∠ACB=90°,
∴∠OCB+∠OCA=90°,
∵∠OBC+∠OCB=90°,
∴∠OCA=∠OBC,
在△OBC和△ECA中 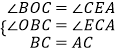 .
.
∴△OBC≌△ECA,
∴OB=CE,
∵AF=OE
∴① ![]() =
= ![]() =
= ![]() =1是定值,
=1是定值,
② ![]() =
= ![]() =
= ![]() =
= ![]() +
+ ![]() =
= ![]() +1,而2AF与AB的关系不知,
+1,而2AF与AB的关系不知,
∴②不是定值.
即:① ![]() 为定值
为定值
【解析】(1)先判断出,∠BCO=∠CAD,从而得出△ACD≌△CBO,求出AD=CO=1,DC=OB=2即可;(2)先利用等腰三角形的判定得出AF=2AE,同(1)的方法判断出△BCD≌△ACF,得出BD=AF即可;(3)作AE⊥OC,同(1)方法判断出△OBC≌△ECA得出OB=CE,最后结合图形求出①个结论是定值.
【考点精析】通过灵活运用等腰三角形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋里,装有4个标号为1,2,3,4的小球;它们大小、材质、形状完全相同,甲从布袋中任意摸出一个小球,记下数字为x,乙从剩下的球中任意摸出一个小球,记下数字为y,以此确定点M的坐标(x,y)。
(l)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=
 的图象上的概率.
的图象上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)20﹣22+(﹣3)3+( )﹣1
)﹣1
(2)(﹣3a3)3a3+(2a3)4﹣(﹣2a6)2
(3)(x+y)2(x﹣y)2
(4)982(用乘法公式计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】P(m+1,5)在y轴上,则m的值为( )
A.﹣5
B.0
C.1
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣(x﹣2)2﹣3的顶点坐标是( )
A.(﹣2,﹣3)
B.(2,3)
C.(﹣2,3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】某电器专卖店策划五一促销活动,已知一款电视机的成本价为1800元/台,专卖店计划将其打七五折销售,同时还要保证每台至少获得10%的利润.若设该款电视机的标价为x元/台,则x满足的不等关系为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)如图①,等边△ABC中,点D是AB边上的一动点(点D与点B不重合),以CD为一边,向上作等边△EDC,连接AE.你能发现线段AE、AD与AC之间的数量关系吗?证明你发现的结论.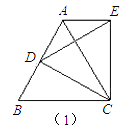
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想线段AE、AD与AC之间的数量关系,并说明理由.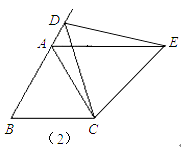
相关试题

