【题目】如图,已知直线l的解析式为y=![]() x﹣1,抛物线y=ax2+bx+2经过点A(m,0),B(2,0),D(1,
x﹣1,抛物线y=ax2+bx+2经过点A(m,0),B(2,0),D(1,![]() )三点.
)三点.

(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;
(2)已知点 P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E,延长PE与直线l交于点F,请你将四边形PAFB的面积S表示为点P的横坐标x的函数,并求出S的最大值及S最大时点P的坐标;
(3)将(2)中S最大时的点P与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.
参考答案:
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2,(﹣4,0).见解析;(2)S的最大值是12,此时点P的坐标为(﹣2,2);(3)见解析
x+2,(﹣4,0).见解析;(2)S的最大值是12,此时点P的坐标为(﹣2,2);(3)见解析
【解析】
试题分析:(1)根据待定系数法可求抛物线的解析式,再根据A(m,0)在抛物线上,得到0=﹣![]() m2﹣
m2﹣![]() m+2,解方程即可得到m的值,从而得到A点的坐标;
m+2,解方程即可得到m的值,从而得到A点的坐标;
(2)根据四边形PAFB的面积S=![]() ABPF,可得S=﹣
ABPF,可得S=﹣![]() (x+2)2+12,根据函数的最值可得S的最大值是12,进一步得到点P的坐标为;
(x+2)2+12,根据函数的最值可得S的最大值是12,进一步得到点P的坐标为;
(3)根据待定系数法得到PB所在直线的解析式为y=﹣![]() x+1,设Q(a,
x+1,设Q(a,![]() a﹣1)是y=
a﹣1)是y=![]() x﹣1上的一点,则Q点关于x轴的对称点为(a,1﹣
x﹣1上的一点,则Q点关于x轴的对称点为(a,1﹣![]() a),将(a,1﹣
a),将(a,1﹣![]() a)代入y=﹣
a)代入y=﹣![]() x+1显然成立,依此即可求解.
x+1显然成立,依此即可求解.
解:(1)∵抛物线y=ax2+bx+2经过点B(2,0),D(1,![]() ),
),
∴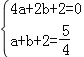 ,
,
解得a=﹣![]() ,b=﹣
,b=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+2,
x+2,
∵A(m,0)在抛物线上,
∴0=﹣![]() m2﹣
m2﹣![]() m+2,
m+2,
解得:m1=﹣4,m2=2(舍去),
∴A点的坐标为(﹣4,0).
如图所示:
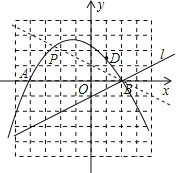
(2)∵直线l的解析式为y=![]() x﹣1,
x﹣1,
∴S=![]() ABPF
ABPF
=![]() ×6PF
×6PF
=3(﹣![]() x2﹣
x2﹣![]() x+2+1﹣
x+2+1﹣![]() x)
x)
=﹣![]() x2﹣3x+9
x2﹣3x+9
=﹣![]() (x+2)2+12,
(x+2)2+12,
其中﹣4<x<0,
∴S的最大值是12,此时点P的坐标为(﹣2,2);
(3)∵直线PB经过点P(﹣2,2),B(2,0),
∴PB所在直线的解析式为y=﹣![]() x+1,
x+1,
设Q(a,![]() a﹣1)是y=
a﹣1)是y=![]() x﹣1上的一点,
x﹣1上的一点,
则Q点关于x轴的对称点为(a,1﹣![]() a),
a),
将(a,1﹣![]() a)代入y=﹣
a)代入y=﹣![]() x+1显然成立,
x+1显然成立,
∴直线l上的任意一点关于x轴的对称点一定在PB所在直线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】剧院的5排4号可以记作(5,4),那么8排3号可以记作__________,(6,5)表示的意义是________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(0,m)在y轴的负半轴上,则点M(﹣m,﹣m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣x+2的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,∠COD=30°.
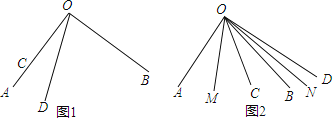
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是 ;
(2)将∠COD从图1的位置开始,绕点O逆时针方向旋转n°(即∠AOC=n°),且0<n<180.
①如果∠COD的一边与∠AOB的一边垂直,则n= .
②当60<n<90时(如图2),作射线OM平分∠AOC,射线ON平分∠BOD,试求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A=∠C﹣∠B
B.a:b:c=2:3:4
C.a2=b2﹣c2
D.a=
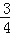 ,b=
,b=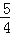 ,c=1
,c=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰△ABC的两边长分别是2和5,则△ABC的周长是( )
A. 9 B. 9或12 C. 12 D. 7或12
相关试题

