搜索
【题目】计算：
（1）（﹣81）+（﹣29）
（2）﹣7+13﹣6+20
（3）1+（﹣
）﹣（﹣
）﹣
（4）﹣0.5﹣（﹣3）+2.75﹣（+7）
（5）（+16）+（﹣3）﹣|﹣8|+|﹣12|﹣（﹣5）
（6）（﹣0.25）×（﹣2）×（﹣
）×（+0.8）
参考答案：
【答案】（1）-110；（2）20；（3）2；（4）﹣1.75；（5）22；（6）﹣
【解析】
（1）根据有理数的加法运算法则计算即可得出答案．
（2）根据有理数加减混合运算法则进行计算即可得出答案；
（3）根据加法的交换律、结合律简便计算，将分母相同的两个数结合起来先相加，再进行计算即可得出答案；
（4）根据有理数的加减混合运算法则进行计算即可得出答案；
（5）先将绝对值化简，再按有理数的加减混合运算法则进行计算即可得出答案；
（6）先把小数化为分数，再根据有理数的乘法运算法则进行计算即可得出答案．
解：（1）原式＝﹣（81+29）＝﹣110
（2）原式＝6﹣6+20＝0+20＝20
（3）原式＝
=
＝1﹣1+2
＝2
（4）原式＝﹣0.5+3+2.75﹣7
＝﹣7.5+5.75
＝﹣1.75
（5）原式＝16+（﹣3）+（﹣8）+12+5
＝33﹣11
＝22
（6）原式＝
＝
-
科目： 来源： 题型：
查看答案和解析>>【题目】进价为每件40元的某商品，售价为每件50元时，每星期可卖出500件，市场调查反映：如果每件的售价每降价1元，每星期可多卖出100件，但售价不能低于每件42元，且每星期至少要销售800件．设每件降价x元 （x为正整数），每星期的利润为y元．
（1）求y与x的函数关系式并写出自变量x的取值范围；
（2）若某星期的利润为5600元，此利润是否是该星期的最大利润？说明理由．
（3）直接写出售价为多少时，每星期的利润不低于5000元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】教师节当天，出租车司机小王在东西向的街道上免费接送教师，规定向东为正，向西为负，当天出租车的行程如下（单位：千米）：
，
，
，
，
，
，
，
．
将最后一名老师送到目的地时，小王距出发地多少千米？方位如何？
若汽车耗油量为
升/千米，则当天耗油多少升？若汽油价格为
元/升，则小王共花费了多少元钱？ -
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数填入它所属的集合内：5.2，0，
，
，+（﹣4），﹣2
，﹣（﹣3 ），0.25555…，﹣0.030030003…（1）分数集合：{_________________________________________ …}
（2）非负整数集合：{_________________________________________ …}
（3）有理数集合：{_________________________________________…}．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，
是
的边
上的中线．（1）①用尺规完成作图：延长
到点
，使
，连接
；② 若
，求的取值范围；（2）如图2，当
时，求证：
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数a、b、c在数轴上的位置如图所示．
（1）化简：|a|＝ |b|＝ ；
（2）比较大小a﹣c 0，a+b 0．
（3）将a，b，c，﹣a，﹣b，﹣c按从小到大的顺序，用“＜”号连接．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直径为1个单位的圆片上有一点A与数轴上的原点重合，AB是圆片的直径．
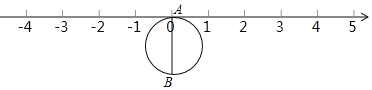
（1）把圆片沿数轴向左滚动1周，点B到达数轴上点C的位置，点C表示的数是 数（填“无理”或“有理”），这个数是 ；
（2）把圆片沿数轴滚动2周，点A到达数轴上点D的位置，点D表示的数是 ；
（3）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：+2，﹣1，+3，﹣4，﹣3
①第几次滚动后，A点距离原点最近？第几次滚动后，A点距离原点最远？
②当圆片结束运动时，A点运动的路程共有多少？此时点A所表示的数是多少？
相关试题
