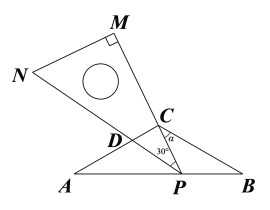
【题目】在△ABC中,CA=CB=3,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由.
(2)在点P滑动的过程中,当AP长度为多少时,△ADP≌△BPC,为什么?
(3)在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若不可以,请说明理由;若可以,请直接写出α的度数.
参考答案:
【答案】(1)直角三角形,理由见解析;(2)当AP=3时,△ADP≌△BPC,理由见解析;(3)当α=45°或90°或0°时,△PCD是等腰三角形
【解析】
(1)由PN与BC平行,得到一对内错角相等,求出∠ACP为直角,即可得证;
(2)当AP=3时,△ADP与△BPC全等,理由为:根据CA=CB,且∠ACB度数,求出∠A与∠B度数,再由外角性质得到∠α=∠APD,根据AP=BC,利用ASA即可得证;
(3)点P在滑动时,△PCD的形状可以是等腰三角形,分三种情况考虑:当PC=PD;PD=CD;PC=CD,分别求出夹角α的大小即可.
(1)当PN∥BC时,∠α=∠NPM=30°,
又∵∠ACB=120°,
∴∠ACP=120°-30°=90°,
∴△ACP是直角三角形;
(2)当AP=3时,△ADP≌△BPC,
理由为:∵∠ACB=120°,CA=CB,
∴∠A=∠B=30°,
又∵∠APC是△BPC的一个外角,
∴∠APC=∠B+α=30°+α,
∵∠APC=∠DPC+∠APD=30°+∠APD,
∴∠APD=α,
又∵AP=BC=3,
∴△ADP≌△BPC;
(3)△PCD的形状可以是等腰三角形,
则∠PCD=120°-α,∠CPD=30°,
①当PC=PD时,△PCD是等腰三角形,
∴∠PCD=∠PDC=![]() =75°,即120°-α=75°,
=75°,即120°-α=75°,
∴∠α=45°;
②当PD=CD时,△PCD是等腰三角形,
∴∠PCD=∠CPD=30°,即120°-α=30°,
∴α=90°;
③当PC=CD时,△PCD是等腰三角形,
∴∠CDP=∠CPD=30°,
∴∠PCD=180°-2×30°=120°,
即120°-α=120°,
∴α=0°,
此时点P与点B重合,点D和A重合,
综合所述:当α=45°或90°或0°时,△PCD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,AD、BD分别平分△ABC的外角∠EAC、内角∠ABC,以下结论:① AD∥BC;②∠ACB=2∠ADB;③ BD⊥AC;④ AC=AD.其中正确的结论有( )

A.①②B.①②④C.①②③D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.
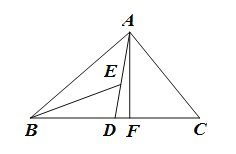
(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
-
科目: 来源: 题型:
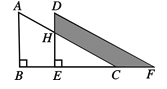
查看答案和解析>>【题目】如图,两个全等的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8, DH=2,平移距离为3,则阴影部分的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC,AB的垂直平分线交线段AC于D,若△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰长和底边BC的长分别是( )
A. 22cm和16cmB. 16cm和22cm
C. 20cm和16cmD. 24cm和12cm
相关试题

