【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG . 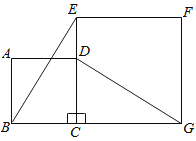
(1)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转过程;若不存在,请说明理由.
(2)观察猜想BE与DG之间的关系,并证明你的结论.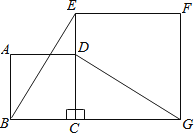
参考答案:
【答案】
(1)
【解答】存在.
∵四边形ABCD和CEFG为正方形,
∴CB=CD,CE=CG,∠BCD=∠ECG=90°,
∴把△CBE绕点C顺时针旋转90°可得△CDG;
(2)
【解答】BE=DG,BE⊥DG.理由如下:
延长GD交BE于M,如图,
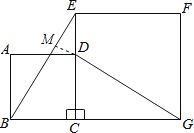
∵△CBE绕点C顺时针旋转90°可得△CDBG,
∴BE=DG,∠BEC=∠DGC,
∵∠BEC+∠CBE=90°,
∴∠BEC+∠DGC=90°,
∴∠BMG=90°,
∴DG⊥BE.
【解析】(1)根据正方形的性质得CB=CD , CE=CG , ∠BCD=∠ECG=90°,则可根据旋转的定义,把△CBE绕点C顺时针旋转90°可得△CDG;(2)根据旋转的性质得BE=DG , ∠BEC=∠DGC , 由于∠BEC+∠CBE=90°,则∠BEC+∠DGC=90°,于是可判断DG⊥BE .
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b,c是三角形的三边,则代数式(a-b)2-c2的值是( )
A. 正数 B. 负数 C. 等于零 D. 不能确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=70°,AC=BC , 以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′B′C , 点A′恰好落在AC上,连接CC′,则∠ACC′=.
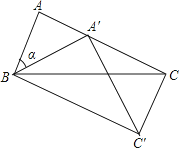
-
科目: 来源: 题型:
查看答案和解析>>【题目】在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多项式9x2-2(m-1)x+16是一个二项式的完全平方式,那么m的值为( )
A. 13 B. -11 C. 7或-5 D. 13或-11
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF=60°,DE、DF分别交AC、BC于E、F点.
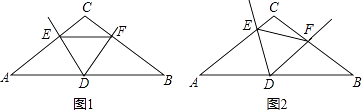
(1)如图1,若EF∥AB.求证:DE=DF.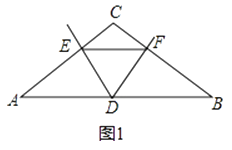
(2)如图2,若EF与AB不平行. 则问题(1)的结论是否成立?说明理由.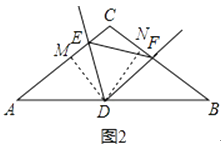
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为t.
①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
相关试题

