【题目】如图,若![]() ,是
,是![]() .
.
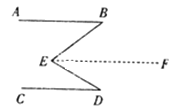
理由:如图,过点![]() 作
作![]() ,
,
则![]() .(依据)
.(依据)
因为![]() ,
,
所以![]() ,
,
所以![]() .
.
所以![]() .
.
(1)上述证明过程中的依据是指 .
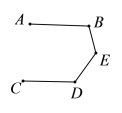
(2)若将点![]() 移至图2所示的位置,
移至图2所示的位置,![]() ,此时
,此时![]() 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.
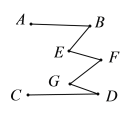
(3)在图中,![]() ,
,![]() 与
与![]() 又有何关系?
又有何关系?
参考答案:
【答案】(1)两直线平等,内错角相等;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)根据两直线平行内错角相等即可得出∠B=∠BEF;
(2)过点E作EF∥AB,由平行线的性质可知∠B+∠BEF=180°,∠D+∠DEF=180°,再由角之间的关系即可得出结论;
(3)过点F作FM∥AB,用(1)的结论可知∠E=∠B+∠EFM,∠G=∠GFM+∠D,再由角之间的关系即可得出结论.
(1)过点E作EF∥AB,
则∠B=∠BEF(两直线平行内错角相等),
故答案为两直线平行内错角相等;
(2)过点E作EF∥AB,如图2所示.
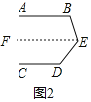
∵AB∥EF,
∴∠B+∠BEF=180°,
∵EF∥AB∥CD,
∴∠D+∠DEF=180°,
∴∠B+∠BEF+∠D+∠DEF=180°+180°,
∵∠E=∠BEF+∠DEF,
∴∠B+∠D+∠E=360°.
(3)过点F作FM∥AB,如图3所示.
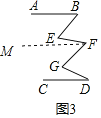
∵AB∥FM,结合(1)结论,
∴∠E=∠B+∠EFM,
∵FM∥AB∥CD,结合(1)结论,
∴∠G=∠GFM+∠D,
又∵∠F=∠EFM+∠GFM,
∴∠E+∠G=∠B+∠D+∠F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,青少年中的近视眼和肥胖案例日趋增多,人们普遍意识到健康的身体是学习的保障,所以体育活动越来越受重视.某商店分两次购进跳绳和足球两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示.
购进数量(件)
购进所需费用(元)
跳绳
足球
第一次
30
40
3800
第二次
40
30
3200
(1)跳绳和足球两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共购进跳绳和足球两种商品100件,其中要求足球的数量不少于跳绳的数量,有哪几种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在4×4的正方形(每个小正方形的边长均为1)网格中,以A为顶点,其他三个顶点都在格点(网格的交点)上,且面积为2的平行四边形共有多少个?( )

A.12B.16C.24D.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.

(1)在正方形网格中,作出△AB1C1;(不要求写作法)
(2)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π).
-
科目: 来源: 题型:
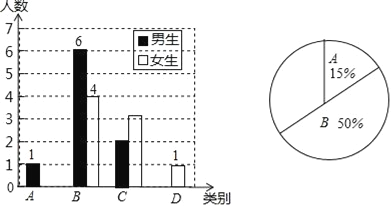
查看答案和解析>>【题目】课前预习是学习的重要环节,为了了解所教班级学生完成课前预习的具体情况,某班主任对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A.优秀,B.良好,C.一般,D.较差,并将调查结果绘制成以下两幅不完整的统计图.
(1)本次调查的样本容量是 ;其中A类女生有 名,D类学生有 名;
(2)将条形统计图和扇形统计图补充完整;
(3)若从被调查的A类和D类学生中各随机选取一位学生进行“一帮一”辅导学习,即A类学生辅导D类学生,请用列表法或画树状图的方法求出所选两位同学中恰好是一位女同学辅导一位男同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=4,BC=6,∠ABC=60°,点P为ABCD内一点,点Q在BC边上,则PA+PD+PQ的最小值为( )
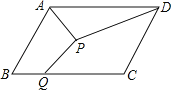
A.
 B.6+2
B.6+2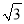 C.5
C.5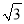 D.10
D.10 -
科目: 来源: 题型:
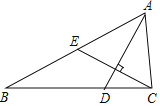
查看答案和解析>>【题目】已知:如图,AD、CE分别是△ABC的角平分线和中线,AD⊥CE,AD=CE=4,则BC的长等于_____.
相关试题

