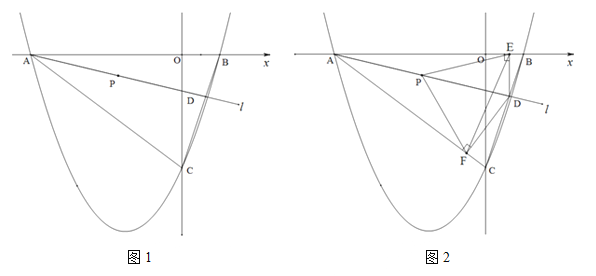
【题目】(2016四川省乐山市第26题)如图1,二次函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,与
轴分别交于A、B两点,与![]() 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程![]() 的两根为-8、2.
的两根为-8、2.
(1)求二次函数的解析式;
(2)直线![]() 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,![]() 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直![]() 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在![]() 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结![]() ,求△PEF周长的最小值.
,求△PEF周长的最小值.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ;②不变,理由见试题解析;(3)
;②不变,理由见试题解析;(3)![]() .
.
【解析】
试题分析:(1)由![]() 与
与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
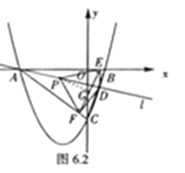
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,故P的运动路程为△ABC的中位线HK,在Rt△BOC中,由勾股定理得到BC的长,再由三角形中位线定理可得到HK的长,即P的运动路程;
②∠EPF的大小不会改变.由于,P为Rt△AED斜边AD的中点,故PE=![]() AD=PA,从而∠PAE=∠PEA=
AD=PA,从而∠PAE=∠PEA=![]() ∠EPD,同理有∠PAF=∠PFA=
∠EPD,同理有∠PAF=∠PFA=![]() ∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=
=PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=![]() ∠EPF=∠BAC,由于tan∠BAC=
∠EPF=∠BAC,由于tan∠BAC=![]() ,故tan∠EPG=
,故tan∠EPG=![]() ,得到EG=
,得到EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,从而有
AD,从而有![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,由
最小,由![]() =30,得到AD=
=30,得到AD=![]() ,从而得到
,从而得到![]() 最小值.
最小值.
试题解析:(1)∵函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入
的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入![]() 中,解得:
中,解得:![]() ,
,![]() ,∴二次函数解析式为:
,∴二次函数解析式为:![]() ;
;
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,∴P的运动路程为△ABC的中位线HK,∴HK=![]() BC,在Rt△BOC中,OB=2,OC=6,∴BC=
BC,在Rt△BOC中,OB=2,OC=6,∴BC=![]() ,∴HK=
,∴HK=![]() ,即P的运动路程为
,即P的运动路程为![]() ;
;
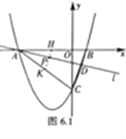
②∠EPF的大小不会改变.理由如下:
∵DE⊥AB,∴在Rt△AED中,P为斜边AD的中点,∴PE=![]() AD=PA,∴∠PAE=∠PEA=
AD=PA,∴∠PAE=∠PEA=![]() ∠EPD,同理可得:∠PAF=∠PFA=
∠EPD,同理可得:∠PAF=∠PFA=![]() ∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF,∵PE=
=PE+PF+EF,∵PE=![]() AD,PF=
AD,PF=![]() AD,∴
AD,∴![]() =AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=
=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=![]() ∠EPF=∠BAC,∵tan∠BAC=
∠EPF=∠BAC,∵tan∠BAC=![]() ,∴tan∠EPG=
,∴tan∠EPG=![]() ,∴EG=
,∴EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,∴
AD,∴![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,∵
最小,∵![]() =30,∴
=30,∴![]() BC·AD=30,∴AD=
BC·AD=30,∴AD=![]() ,∴
,∴![]() 最小值为:
最小值为:![]() AD=
AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠A=50°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题探究】用同样大小的小正方形纸片,按下图的方式拼正方形.
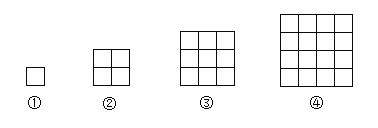
规律:第①个图形中有1个小正方形;
第②个图形比第①个图形多3个小正方形;
第③个图形比第②个图形多5个小正方形;
……
第(n+1)个图形比第n个图形多________个小正方形.
可发现以下结论:(1)1+3+5+…+(2n-1)= ____________.
(2)(n+1)2-n2 = ____________.
【知识运用】
运用一:如果一个数可用几个连续的奇数和来表示,我们称这个数为“好数”,例如:9=1+3+5,32=5+7+9+11,则称9和32都是“好数”.
请尝试将下列“好数”用连续奇数的和表示出来:
(1)
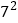 =_____________________________________.
=_____________________________________.(2)99 =_____________________________________.
运用二:利用上面的结论,请计算
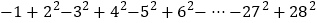 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖北襄阳第23题)
襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:

(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
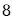 ,某无人机于空中
,某无人机于空中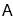 处探测到目标
处探测到目标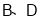 的俯角分别是
的俯角分别是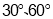 ,此时无人机的飞行高度
,此时无人机的飞行高度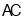 为
为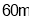 ,随后无人机从
,随后无人机从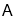 处继续水平飞行
处继续水平飞行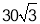 m到达
m到达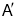 处.
处.(1)求
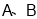 之间的距离
之间的距离(2)求从无人机
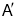 上看目标
上看目标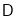 的俯角的正切值.
的俯角的正切值.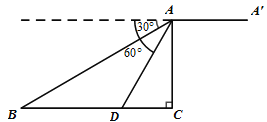
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张)
零售价(元/张)
成套售价(元/套)
餐桌
a
270
500元
餐椅
a﹣110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(2)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(2)中的最大利润少了2250元.请问本次成套的销售量为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2+x﹣2=0,则方程的两根为 .
相关试题

