【题目】【问题探究】用同样大小的小正方形纸片,按下图的方式拼正方形.
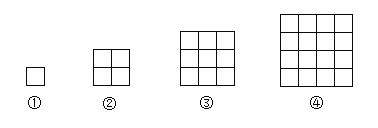
规律:第①个图形中有1个小正方形;
第②个图形比第①个图形多3个小正方形;
第③个图形比第②个图形多5个小正方形;
……
第(n+1)个图形比第n个图形多________个小正方形.
可发现以下结论:(1)1+3+5+…+(2n-1)= ____________.
(2)(n+1)2-n2 = ____________.
【知识运用】
运用一:如果一个数可用几个连续的奇数和来表示,我们称这个数为“好数”,例如:9=1+3+5,32=5+7+9+11,则称9和32都是“好数”.
请尝试将下列“好数”用连续奇数的和表示出来:
(1)![]() =_____________________________________.
=_____________________________________.
(2)99 =_____________________________________.
运用二:利用上面的结论,请计算![]() 的值.
的值.
参考答案:
【答案】 (2n+1) n2 2n+1 1+3+5+7+9+11+13 3+5+7+9+11+13+15+17+19 或 31+33+35
【解析】试题分析:
【问题探究】
第②个图形比第①个图形多3=2×2-1个小正方形;
第③个图形比第②个图形多5=2×3-1个小正方形;
……
第n个图形比第n-1个图形多2n-1个小正方形
第(n+1)个图形比第n个图形多2(n+1)-1=2n+1个小正方形;
(1)1+3+5+…+(2n-1)表示第n个图形的小正方形个数,所以1+3+5+…+(2n-1)=n2;
(2)(n+1)2-n2表示第(n+1)个图形比第n个图形多的小正方形个数,所以(n+1)2-n2=2n+1.
【知识运用】
运用一:
(1)由以上可知1+3+5+…+(2n-1)=n2,令n=7,则有72=1+3+5+7+9+11+13;
(2)99=100-1
=102-1
=1+3+5+…+19-1
=3+5+…+19;
或99=182-152
=(1+3+5+…+35)-(1+3+5+…+29)
=31+33+35;
运用二:
将原式每两项分为一组,然后利用前面发现的规律(n+1)2-n2=2n+1进行解答即可.
试题解析:
【问题探究】
第(n+1)个图形比第n个图形多 (2n+1) 个小正方形.
可发现以下结论:(1)1+3+5+…+(2n-1)= n2 .
(2)(n+1)2-n2 = 2n+1 .
【知识运用】
运用一:
(1)72= 1+3+5+7+9+11+13 .
(2)99 = 3+5+7+9+11+13+15+17+19 或 31+33+35 .(填一种即可)
运用二:
(法一):原式=(22-1)+(42-32)+(62-52)+…+(282-272)
=(2×1+1)+(2×3+1)+(2×5+1)+…+(2×27+1)
= 2×(1+3+5+…+27)+14
= 2×196+14
= 406
(法二):原式= (22-1)+(42-32)+(62-52)+…+(282-272)
= 1+2+3+4+5+6+…+27+28
= ![]()
= 406
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100°
B.160°
C.80°
D.60° -
科目: 来源: 题型:
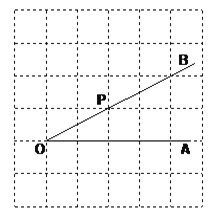
查看答案和解析>>【题目】如图,点P是
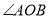 的边OB上的一点。
的边OB上的一点。过点P画OA的垂线,垂足为H;
过点P画OB的垂线,交OA于点C;
线段PH的长度是点P到 的距离,_____ 是点C到直线OB的距离。因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 。(用“<”号连接)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠A=50°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖北襄阳第23题)
襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:

(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016四川省乐山市第26题)如图1,二次函数
 的图象与
的图象与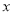 轴分别交于A、B两点,与
轴分别交于A、B两点,与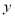 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程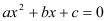 的两根为-8、2.
的两根为-8、2.(1)求二次函数的解析式;
(2)直线
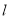 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,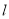 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.①求点P的运动路程;
②如图2,过点D作DE垂直
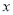 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在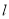 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;(3)在(2)的条件下,连结
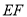 ,求△PEF周长的最小值.
,求△PEF周长的最小值.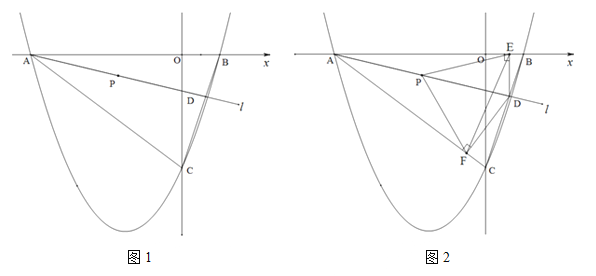
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,某无人机于空中
,某无人机于空中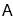 处探测到目标
处探测到目标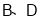 的俯角分别是
的俯角分别是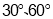 ,此时无人机的飞行高度
,此时无人机的飞行高度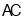 为
为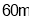 ,随后无人机从
,随后无人机从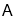 处继续水平飞行
处继续水平飞行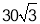 m到达
m到达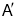 处.
处.(1)求
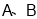 之间的距离
之间的距离(2)求从无人机
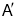 上看目标
上看目标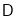 的俯角的正切值.
的俯角的正切值.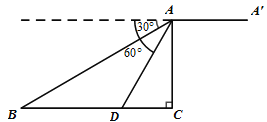
相关试题

