【题目】如图,点![]() 为⊙
为⊙![]() 上一点,点
上一点,点![]() 在直径
在直径![]() 的延长线上,且
的延长线上,且![]() .
.
(1)判断直线![]() 和⊙
和⊙![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)过点![]() 作⊙
作⊙![]() 的切线
的切线![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,⊙
,⊙![]() 的半径是
的半径是![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)直线CD和⊙O的位置关系是相切,理由见解析;(2)6.
【解析】试题分析:(1)连接OD,根据圆周角定理求出∠DAB+∠DBA=90°,求出∠CDA+∠ADO=90°,根据切线的判定推出即可;
(2)根据勾股定理求出DC,根据切线长定理求出DE=EB,根据勾股定理得出方程,求出方程的解即可.
试题解析:(1)直线CD和⊙O的位置关系是相切,
理由是:连接OD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即OD⊥CE,
已知D为⊙O的一点,
∴直线CD是⊙O的切线,
即直线CD和⊙O的位置关系是相切;
(2)∵AC=2,⊙O的半径是3,
∴OC=2+3=5,OD=3,
在Rt△CDO中,由勾股定理得:CD=4,
∵CE切⊙O于D,EB切⊙O于B,
∴DE=EB,∠CBE=90°,
设DE=EB=x,
在Rt△CBE中,由勾股定理得:CE2=BE2+BC2,
则(4+x)2=x2+(5+3)2,
解得:x=6,
即BE=6.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A、不是负数的数是正数 B、正数和负数构成有理数
C、整数和分数构成有理数 D、正整数和负整数构成整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有三角形“▲"和“△”共2011个,按照一定的规律排列如下: ▲△△▲△▲▲△△▲△▲▲…….,则黑色三角形共有_____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中不正确的是( )
A.在同一平面内,经过一点能而且只能画一条直线与已知直线垂直
B.一条线段有无数条垂线
C.在同一平面内过射线的端点只能画一条直线与这条射线垂直
D.如果直线AB垂直平分线段CD,那么CD也垂直平分AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则
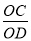 的值为( )
的值为( )
A.
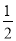 B.
B.  C.
C. 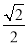 D.
D. 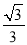
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x1,y1)·(x2,y2)=x1x2+y1y2,则(4,5)·(6,8)=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.三角形三条角平分线的交点叫重心
B.三角形三条高交于一点
C.面积相等的两个三角形一定全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
相关试题

