【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;证明: 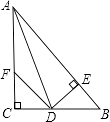
(1)CF=EB.
(2)AB=AF+2EB.
参考答案:
【答案】
(1)证明:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,
![]() ,
,
∴Rt△CDF≌Rt△EDB(HL).
∴CF=EB
(2)证明:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,
![]() ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
【解析】(1)根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即CD=DE.再根据Rt△CDF≌Rt△EDB,得CF=EB;(2)利用角平分线性质证明∴△ADC≌△ADE,AC=AE,再将线段AB进行转化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(2m+1)2-(2m+1)(2m-1);
(2)(2x+y-3z)2-(2x-y+3z)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(4,6),B(5,2),C(2,1),

(1)作出△ABC关于y轴对称的△A′B′C′,并写出A′,B′,C′的坐标.
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 一次函数是正比例函数
B. 正比例函数是一次函数
C. 不是正比例函数就一定不是一次函数
D. 正比例函数不一定是一次函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)可能性最大和最小的事件分别是哪个?(填写序号)
(2)将这些事件的序号按发生的可能性从小到大的顺序排列: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
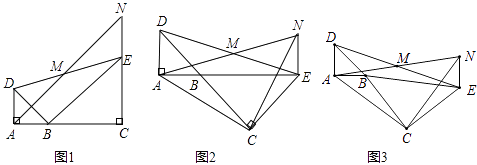
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式能用完全平方公式进行分解因式的是( )
A.x2+1
B.x2+2x﹣1
C.x2+x+1
D.x2+4x+4
相关试题

