搜索
【题目】填写下表
序号 |
| 1 | 2 | … |
① |
| 5 |
| … |
② |
| 2 |
| … |
③ |
|
| 4 | … |
随着
值的逐渐变大，回答下列问题
（1）当
时，这三个代数式中 的值最小；
（2）你预计代数式的值最先超过1000的是代数式 ，此时的值为 ．
参考答案：
【答案】表格见解析；（1）
；（2）
，10
【解析】
将n=1和2分别代入三个代数式计算即可填表；
（1）当n=5时，分别代入各个代数式计算即可得到答案；
（2）预计得到最先超过1000的，求出n的值即可．
解：填表：当n=2时，
，
；当n=1时，
，
故表格如下：
（1）当n=5时，4n＋1=4×5＋1=21，n2＋1=25＋1=26，2n=25=32，
∵32＞26＞21，
∴当n=5时，4n＋1的值最小．
故答案为：；
（2）预计代数式的值最先超过1000的是2n；此时n的值为10．
故答案为：，10．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在某地，人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的近似关系：用蟋蟀1min叫的次数除以7，然后再加上3，就近似地得到该地当时的温度（℃）．
（1）用代数式表示该地当时的温度；
（2）当蟋蟀1min叫的次数分别是84，105和126时，该地当时的温度约是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】世界杯比赛中，根据场上攻守形势，守门员会在门前来回跑动，如果以球门线为基准，向前跑记作正数，返回则记作负数，一段时间内，某守门员的跑动情况记录如下（单位：m）：+10，﹣2，+5，﹣6，+12，﹣9，+4，﹣14．（假定开始计时时，守门员正好在球门线上）
（1）守门员最后是否回到球门线上？
（2）守门员离开球门线的最远距离达多少米？
（3）如果守门员离开球门线的距离超过10米（不包括10米），则对方球员挑射极可能造成破门．请问在这一时间段内，对方球员有几次挑射破门的机会？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校初三（1）班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题．
（1）初三（1）班接受调查的同学共有多少名；
（2）补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数；
（3）若喜欢“交流谈心”的5名同学中有三名男生和两名女生；老师想从5名同学中任选两名同学进行交流，直接写出选取的两名同学都是女生的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，△ABC，∠ACB=90°，AC=5，DE⊥BD，BC=BD，∠ABE=∠CBD.
（1）求证：△ABC≌△EBD
（2）延长AC交DE于F点，若BC⊥BD，CF=4，求EF的长度.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某大楼的顶部树有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知山坡AB的坡度i=1：
，AB=10米，AE=15米．（i=1：是指坡面的铅直高度BH与水平宽度AH的比）
（1）求点B距水平面AE的高度BH；
（2）求广告牌CD的高度．
（测角器的高度忽略不计，结果精确到0.1米．参考数据：
1.414，
1.732） -
科目： 来源： 题型：
查看答案和解析>>【题目】（问题情境）学习《探索全等三角形条件》后，老师提出了如下问题：如图①，△ABC中，若AB=12，AC=8，求BC边上的中线AD的取值范围。同学通过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，连接BE.根据SAS可证得到△ADC≌△EDB，从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.
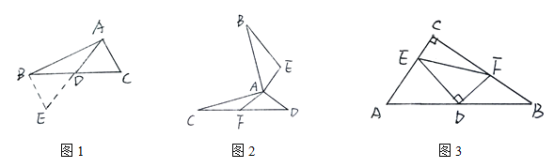
（直接运用）如图②，AB⊥AC，AD⊥AE，AB=AC，AD=AE，AF是ACD的边CD上中线.求证：BE=2AF.
（灵活运用）如图③，在△ABC中，∠C=90°，D为AB的中点，DE⊥DF，DE交AC于点E，DF交AB于点F，连接EF，试判断以线段AE、BF、EF为边的三角形形状，并证明你的结论.
相关试题
