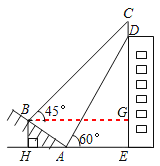
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
参考答案:
【答案】解:(1)过B作BG⊥DE于G,
在Rt△ABF中,i=tan∠BAH=![]() ,∴∠BAH=30°
,∴∠BAH=30°
∴BH=![]() AB=5(米)。
AB=5(米)。
答:点B距水平面AE的高度BH为5米。
(2)由(1)得:BH=5,AH=5![]() ,
,
∴BG=AH+AE=5![]() +15。
+15。
在Rt△BGC中,∠CBG=45°,∴CG=BG=5![]() +15。
+15。
在Rt△ADE中,∠DAE=60°,AE=15,
∴DE=![]() AE=15
AE=15![]() 。
。
∴CD=CG+GE﹣DE=5![]() +15+5﹣15
+15+5﹣15![]() =20﹣10
=20﹣10![]() ≈2.7(米)。
≈2.7(米)。
答:宣传牌CD高约2.7米。
【解析】
试题(1)过B作DE的垂线,设垂足为G.分别在Rt△ABH中,通过解直角三角形求出BH、AH。
(2)在△ADE解直角三角形求出DE的长,进而可求出EH即BG的长,在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE﹣DE即可求出宣传牌的高度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】填写下表
序号

1
2
…
①
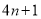
5
…
②
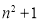
2
…
③
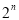
4
…
随着
 值的逐渐变大,回答下列问题
值的逐渐变大,回答下列问题(1)当
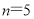 时,这三个代数式中 的值最小;
时,这三个代数式中 的值最小;(2)你预计代数式的值最先超过1000的是代数式 ,此时
 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC,∠ACB=90°,AC=5,DE⊥BD,BC=BD,∠ABE=∠CBD.

(1)求证:△ABC≌△EBD
(2)延长AC交DE于F点,若BC⊥BD,CF=4,求EF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)学习《探索全等三角形条件》后,老师提出了如下问题:如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围。同学通过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.根据SAS可证得到△ADC≌△EDB,从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
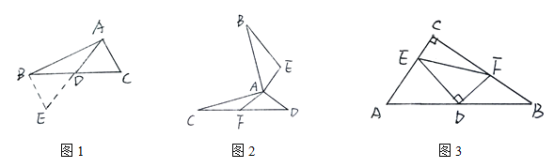
(直接运用)如图②,AB⊥AC,AD⊥AE,AB=AC,AD=AE,AF是ACD的边CD上中线.求证:BE=2AF.
(灵活运用)如图③,在△ABC中,∠C=90°,D为AB的中点,DE⊥DF,DE交AC于点E,DF交AB于点F,连接EF,试判断以线段AE、BF、EF为边的三角形形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).
(1)用代数式表示(所填式子需化简):当购买乒乓球的盒数为
 盒时,在甲店购买需付款 元;在乙店购买需付款 元.
盒时,在甲店购买需付款 元;在乙店购买需付款 元.(2)当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.
(3)当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
 是长方形,面积为
是长方形,面积为
(1)如图1,
 是
是 边上一点,连接
边上一点,连接 、
、 ,则三角形
,则三角形 的面积为 (用含
的面积为 (用含 的代数式表示).
的代数式表示).(2)
 是长方形
是长方形 内一点,连接
内一点,连接 、
、 、
、 、
、 ,三角形
,三角形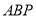 的面积为
的面积为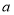 .
.①如图2,则三角形
 的面积为 ;(用含
的面积为 ;(用含 、
、 的代数式表示)
的代数式表示)②如图3,连接
 ,若三角形
,若三角形 的面积为
的面积为 ,则三角形
,则三角形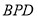 的面积为 .(用含
的面积为 .(用含 的代数式表示)
的代数式表示)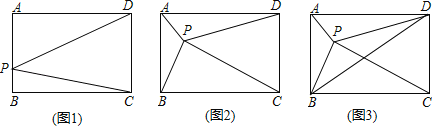
相关试题

