【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3cm,设运动的时间为t秒.
(1)当t= 时,CP把△ABC的周长分成相等的两部分?
(2)当t= 时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为18?

参考答案:
【答案】(1)4;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 的面积为18.
的面积为18.
【解析】
(1)先根据CP把![]() 的周长分成相等的两部分可知,此时点P在边AB上,再根据线段的和差建立等式求解即可;
的周长分成相等的两部分可知,此时点P在边AB上,再根据线段的和差建立等式求解即可;
(2)先根据三角形的中线的性质确定点P的位置,从而可得AP的长,再根据线段的和差求出![]() 的长,由此即可得出答案;
的长,由此即可得出答案;
(3)分点P在边AC上和点P在边AB上两种情况,然后分别利用三角形的面积公式列出等式求解即可.
(1)由题意可知,只有当点P在边AB上,CP才能把![]() 的周长分成相等的两部分
的周长分成相等的两部分
则![]()
![]() 点P的运动速度为每秒
点P的运动速度为每秒![]()
![]()
![]()
![]()
则有![]()
解得![]()
即当![]() 时,CP把
时,CP把![]() 的周长分成相等的两部分
的周长分成相等的两部分
故答案为:4;
(2)当点P为AB中点时,由三角形的中线性质可知,此时![]() ,即CP把
,即CP把![]() 的面积分成相等的两部分
的面积分成相等的两部分
则![]()
由![]() 得:
得:![]()
解得![]()
故答案为:![]() ;
;
(3)点P运动至点A所需时间为![]() 秒,点P运动至点B所需时间为
秒,点P运动至点B所需时间为![]() (秒)
(秒)
由题意,分以下两种情况:
①当点P在边AC上,即![]() 时
时
![]()
则![]() ,即
,即![]()
解得![]() ,符合题设
,符合题设
②当点P在边AB上,即![]() 时
时
由(1)可知,![]()
如图,过点C作![]() 于点D
于点D
由![]() 的面积得:
的面积得:![]() ,即
,即![]()
解得![]()
则![]() ,即
,即![]()
解得![]() ,符合题设
,符合题设
综上,当![]() 或
或![]() 时,
时,![]() 的面积为18.
的面积为18.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)
 ;
;(2)(﹣a)3a2+(2a4)2÷a3;
(3)(2x﹣y)2﹣(y+x)(y﹣x);
(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,8×8的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.将△ABC经过一次平移后得到△A′B′C′,点B′是点B的对应点.
(1)△ABC的面积是 ;
(2)画出平移后得到的△A′B′C′;
(3)画出△ABC的高线CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )
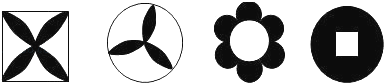
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个半径为r的圆形纸片在边长为a(
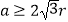 )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )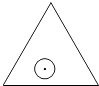
A.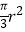
B.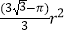
C.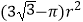
D.πr2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知在△ABC中,∠BAC=40°,BD⊥AC于D,CE⊥AB于E,BD、CE所在直线交于点F,求∠BFC的度数;
(2)在(1)的基础上,若∠BAC每秒扩大10°,且在变化过程中∠ABC与∠ACB始终保持是锐角,经过t秒(0<t<14),在∠BFC,∠BAC这两个角中,当一个为另一个的两倍时,求t的值;
(3)在(2)的基础上,∠ABD与∠ACE的角平分线交于点G,∠BGC是否为定值,如果是,请直接写出∠BGC的值,如果不是,请写出∠BGC是如何变化的.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE与射线AF交于点G.若OE将∠BOA分成1︰2两部分,AF平分∠BAD,∠ABO=
 (30°<
(30°<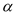 <90°) ,则∠OGA的度数为(用含
<90°) ,则∠OGA的度数为(用含 的代数式表示)____________________.
的代数式表示)____________________.
相关试题

