搜索
【题目】如图，一个半径为r的圆形纸片在边长为a（ 
）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）
A.
B.
C.
D.πr2
参考答案：
【答案】C
【解析】如图，当圆形纸片运动到与
A的两边相切的位置时，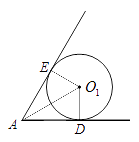
过圆形纸片的圆心O1作两边的垂线，垂足分别为D，E，
连接AO1，则Rt
ADO1中，O1AD=30
，O1D=r，AD=
r，
∴SADO1=
O1D
AD=
r2，由此S四边形ADO1E=2SADO1=r2，
∵由题意，DO1E=120，得S扇形O1DE=
r2，
∴圆形纸片“不能接触到的部分”的面积是3（r2-r2）=（
）r2 .
所以答案是：C.
【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，8×8的正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的顶点都在正方形网格的格点上．将△ABC经过一次平移后得到△A′B′C′，点B′是点B的对应点．
（1）△ABC的面积是 ；
（2）画出平移后得到的△A′B′C′；
（3）画出△ABC的高线CD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（ ）
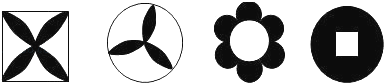
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，AB＝10cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒3cm，设运动的时间为t秒．
（1）当t＝ 时，CP把△ABC的周长分成相等的两部分？
（2）当t＝ 时，CP把△ABC的面积分成相等的两部分？
（3）当t为何值时，△BCP的面积为18？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图，已知在△ABC中，∠BAC＝40°，BD⊥AC于D，CE⊥AB于E，BD、CE所在直线交于点F，求∠BFC的度数；
（2）在（1）的基础上，若∠BAC每秒扩大10°，且在变化过程中∠ABC与∠ACB始终保持是锐角，经过t秒（0＜t＜14），在∠BFC，∠BAC这两个角中，当一个为另一个的两倍时，求t的值；
（3）在（2）的基础上，∠ABD与∠ACE的角平分线交于点G，∠BGC是否为定值，如果是，请直接写出∠BGC的值，如果不是，请写出∠BGC是如何变化的．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，∠COD=90°，直线AB与OC交于点B，与OD交于点A，射线OE与射线AF交于点G．若OE将∠BOA分成1︰2两部分，AF平分∠BAD，∠ABO=
（30°<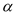
<90°） ，则∠OGA的度数为（用含的代数式表示)____________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，已知抛物线与直线的图象如图所示，当y1≠y2时，取y1 ， y2中的较大值记为N；当y1=y2时，N=y1=y2 ． 则下列说法：
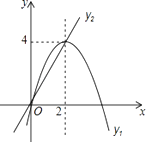
①当0＜x＜2时，N=y1；
②N随x的增大而增大的取值范围是x＜0；
③取y1 ， y2中的较小值记为M，则使得M大于4的x值不存在；
④若N=2，则x=2﹣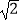
或x=1．
其中正确的有（ ）
A.1个
B.2个
C.3个
D.4个
相关试题
